O Viche tem recebido visitas a partir de pesquisas efetuadas no Google com o termo triângulo em função dos artigos publicados sobre Tecelagem Popular no Triângulo Mineiro. Assim, com o objetivo de atender esse indicativo presente nas estatísticas do blog passo a escrever sobre conceitos relacionados ao termo mencionado: mais especificamente sobre Semelhança entre Triângulos.
Antes, vamos definir o que é congruência entre triângulos.
Congruência entre Triângulos
Dois triângulos (ou de forma geral, duas figuras planas) são congruentes quando têm a mesma forma e as mesmas dimensões, ou seja, o mesmo tamanho.
Já a semelhança entre triângulos, objeto do artigo, aborda o conceito mais amplo onde se tem triângulos com a mesma forma, mas não necessariamente com o mesmo tamanho. Em outras palavras, congruência é um caso particular de semelhança entre triângulos no sentido de que se dois triângulos são congruentes necessariamente eles são semelhantes, mas o contrário não é verdadeiro, como você observará daqui em diante.
Definição de Semelhança entre Triângulos
Dizemos que dois triângulos são semelhantes se, e somente se, possuem seus três ângulos ordenadamente congruentes e os lados homólogos (homo = mesmo, logos = lugar) proporcionais.
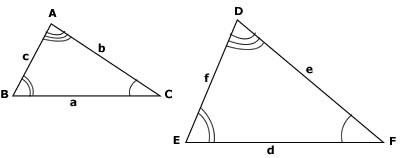
Traduzindo a definição em símbolos:
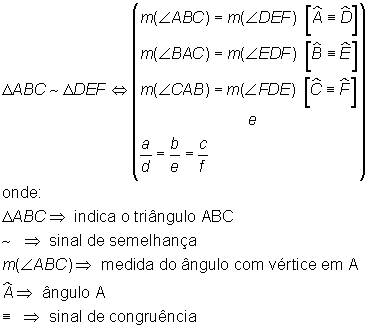
Observe que as três primeiras expressões entre os parêntesis indicam a congruência ordenada dos ângulos e a última a proporcionalidade dos lados homólogos.
Em bom português, podemos, ainda, definir a semelhança entre triângulos através da frase: dois triângulos são semelhantes se um pode ser obtido pela expansão uniforme do outro (caso deseje comprovar veja o programa em Java descrito abaixo).
Razão de Semelhança
Denominamos o número real k, que satisfaz as igualdades abaixo entre os lados homólogos, como a razão de semelhança dos triângulos:

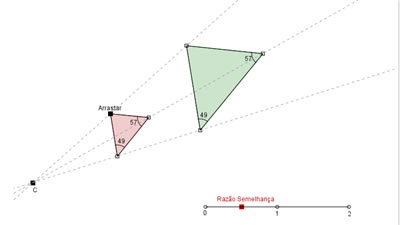
Para uma idéia melhor dos conceitos acima sugiro uma visita ao programa em Java de Karlos Gomes. A imagem inicial da página é apresentada a seguir, onde temos dois triângulos entre um feixe de três retas com origem no ponto C. Ao arrastar o triângulo rosa para cima ou para baixo, o ponto em vermelho no segmento de reta indica o valor da razão de semelhança correspondente. Ao colocar o triângulo rosa exatamente sobre o verde você observará que a razão de semelhança é igual a 1, como era de se esperar (você sabe dizer o significado deste fato?).
O único problema é que o programa demora a carregar. Tenha um pouco de paciência, e espere, vale a pena. Após, por favor, retorne a este artigo :-).
Exemplo
Dados os triângulos ABC e DEF semelhantes com as medidas dos lados indicadas abaixo, calcule as medidas dos lados e e d do segundo triângulo.
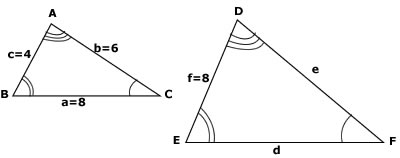
Solução:
Como os triângulos são semelhantes por hipótese, vem, pela razão de semelhança, que:
c = kf => k = c/f => k = 4/8 = 1/2
De forma análoga:
a = kd => 8 = (1/2)d => d = 16
b = ke => 6 =(1/2)e => e = 12
Propriedades
a) Reflexiva: Todo triângulo é semelhante a si próprio.
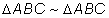
b) Simétrica: Se um triângulo é semelhante a um outro, este é semelhante ao primeiro.

c) Transitiva: Se um triângulo é semelhante a um segundo e este é semelhante a um terceiro, então o primeiro é semelhante ao terceiro.
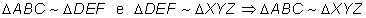
Teorema Fundamental
Se uma reta é paralela a um dos lados de um triângulo e intercepta os outros dois em pontos distintos, então o triângulo que ela determina é semelhante ao primeiro.
A demonstração do Teorema Fundamental é feita a partir do Teorema de Tales, que por sua vez pode ser demonstrado a partir dos critérios de semelhança definidos abaixo (fica como exercício).
Se um feixe de retas paralelas tem duas transversais, então a razão entre dois segmentos quaisquer de uma é igual à razão entre os segmentos correspondentes na outra.
Demonstração do Teorema Fundamental:
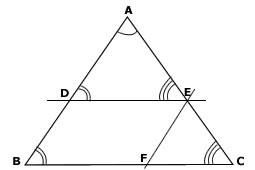
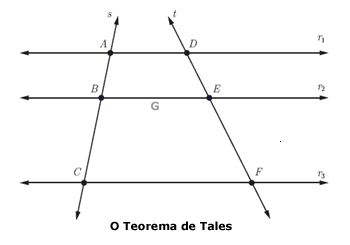
A demonstração da congruência dos ângulos dos triângulos ABC e ADE (figura abaixo) decorre do fato de que ângulos correspondentes determinados por duas paralelas são congruentes. Assim, o ângulo B é congruente ao D e o ângulo C é congruente ao E. Como o ângulo A é comum aos dois triângulos concluímos a primeira parte da demonstração.
Pelo Teorema de Tales temos que:
m(AD)/m(AB) = m(AE)/m(AC) [1]
Por E construímos a reta EF paralela a BD, conforme indicado na figura acima. Do paralelogramo BDEF temos que m(DE) = m(BF). E, novamente, pelo Teorema de Tales:
m(AE)/m(AC) = m(BF)/m(BC) => m(AE)/m(AC) = m(DE)/m(BC) [2]
De [1] e [2] vem que os lados homólogos são proporcionais, o que conclui a demonstração.
Observação: Nos termos do tipo m(AE), utlizados acima, imagine uma barra sobre AE para se ter a notação correta conforme indicado anteriormente.
Critérios de Semelhança de Triângulos
Critério AA => Ângulo-Ângulo: Se dois triângulos têm dois ângulos internos correspondentes congruentes, então os triângulos são semelhantes.
Demonstração:
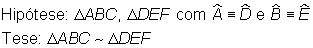 No caso dos dois triângulos serem congruentes, nada há a demonstrar, pois por definição de congruência os triângulos são necessariamente semelhantes. Suponhamos, então, como indicado na figura, o triângulo ABC maior que o triângulo DEF e construamos o triângulo AGH tal que a medida do lado AG seja igual à medida do lado DE, o ângulo G congruente ao ângulo E e H sobre o lado AC.
No caso dos dois triângulos serem congruentes, nada há a demonstrar, pois por definição de congruência os triângulos são necessariamente semelhantes. Suponhamos, então, como indicado na figura, o triângulo ABC maior que o triângulo DEF e construamos o triângulo AGH tal que a medida do lado AG seja igual à medida do lado DE, o ângulo G congruente ao ângulo E e H sobre o lado AC.
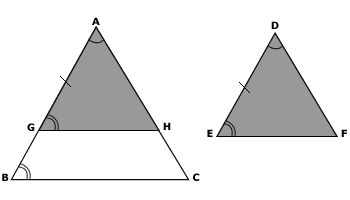
Além disso, como o ângulo A é congruente ao ângulo D, por hipótese, o triângulo AGH é congruente ao triângulo DEF (critério ALA da congruência entre triângulos) e portanto semelhantes.
Por outro lado, pelo Teorema Fundamental, temos que o triângulo AGH é semelhante ao triângulo ABC, já que o lado GH é paralelo ao lado BC. E, finalmente, como o triângulo ABC é semelhante ao triângulo AGH, e AGH, por sua vez, é semelhante a DEF, concluímos, pela propriedade transitiva, que o triângulo ABC é semelhante ao triângulo DEF.
As demonstrações dos demais critérios ficam como exercício.
Critério AAA => Ângulo-Ângulo-Ângulo: Se os ângulos de um triângulo forem respectivamente congruentes aos ângulos correspondentes de outro triângulo, então os triângulos são semelhantes.
Critério LAL => Lado-Ângulo-Lado: Se as medidas de dois dos lados de um triângulo são proporcionais aos homólogos do outro triângulo e os ângulos determinados por estes lados são congruentes, então os triângulos são semelhantes.
Critério LLL => Lado-Lado-Lado: Se as medidas dos lados de um triângulo são respectivamente proporcionais às medidas dos lados correspondentes de outro triângulo, então os triângulos são semelhantes.
Teorema de Pitágoras
Um triângulo é denominado retângulo se um de seus ângulos é reto, ou seja, tem 90 graus. O lado de maior medida é denominado hipotenusa (a) e os outros dois lados de catetos (b e c).
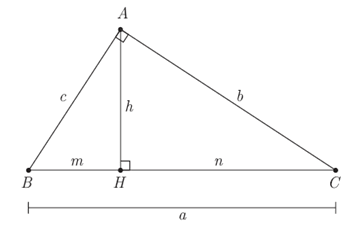
Pitágoras estabeleceu, então, em seu mais famoso teorema que: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos, i.e.:
a2 = b2 + c2
Para finalizar o artigo com chave de ouro vamos demonstrar o Teorema de Pitágoras com o uso dos critérios de semelhança.
Demonstração:
Observe que os triângulos ABH e ABC são semelhantes como decorrência do critério AA, uma vez que ambos possuem um ângulo reto e o ângulo B em comum. Daí tiramos a seguinte relação entre os lados homólogos:
c/a = m/c => c2 = a.m => c2 = a.(a – n) => c2 = a2 – an [1]
Pela mesma razão os triângulos AHC e ABC são semelhantes. Logo:
b/a = n/b => b2 = an [2]
Substituindo [2] em [1] vem que:
c2 = a2 – b2 => a2 = b2 + c2.




mar 25, 2008 @ 09:06:09
Adoreiiiii Ameiiii
virei fãããã
mar 25, 2008 @ 09:01:34
achei o maximo!!!!!!!!!!!!
mar 24, 2008 @ 20:00:45
Esse conteúdo foi muito bem resumido e claro para aqueles que estudam, mas vocês poderiam colocar alguns testes instantâneos avaliativos, valendo de zero a dez.
mar 17, 2008 @ 20:19:00
salvou minha vida..!!
shauhsuahsua
super bem explicado!
gostei muito
mar 06, 2008 @ 20:48:47
Não fOi o q eu esperava
procurava mais explicaçoes e não encontrei
pedi exercícios com explicações
não foi o q vi
espero q melhore
desde já agradeço
mar 06, 2008 @ 18:12:53
Estudando por aqui achei que a matéria é mais complicada.
Mas ajudou !!
fev 23, 2008 @ 15:28:27
foi o k mais me interessou
fev 18, 2008 @ 12:19:39
ótimo! resolveu meu problema.
fev 10, 2008 @ 13:06:52
nao foi o que eu estava proucurando… nao deu pra entender muito sobre o assunto…obrigada
dez 30, 2007 @ 20:10:02
qual deste e o criterio fundamental dasemelhanca de triangulos:
angulo-lado, lado-lado, angulo-angulo ou lado-angulo um hexaedro quantas faces,arestas vertices tem? obrigado aguardo resposta. boa noite e bom final de ano.
nov 23, 2007 @ 09:53:09
Égua você(s) que fez esse site você(s) esta(ão) de parabens, esse site é muito bom este site tem tudo que eu queria muito obrigado!!!
nov 18, 2007 @ 15:03:29
Adorei a maneira que abordaram o assunto , me ajudou muito no meu trabalho de escola!!
Parabéns
nov 16, 2007 @ 08:59:21
po eu nu gostei não por q eu não achei a propriedade fundamental da semelhança de triangulos.
nov 12, 2007 @ 17:56:39
QUERIA UMA COISA MAIS APRIMORADO!!!
MAIS É UMA ÓTIMA EXPLICAÇÃO!!!
MUITO BOA MESMO!!
nov 08, 2007 @ 19:23:02
Olá meu nome é Vanessa tenho 16 anos e por ter dificuldade em matemática recorri a esse site que na verdade não me ajudou muito.Queria deixar uma sugestão:Seria melhor se vc’s se aprofundassem nos assuntos ou explicassem mais.
nov 08, 2007 @ 12:18:35
Maravilhosa as explicações sobre o teorema de Tales, gostei muito e me ajudou a melhorar a forma de expor o assunto para os meus alunos. Parabéns pela clareza das explicações.
nov 08, 2007 @ 12:06:41
adorei,pois tive muitas duvidas na materia TEOREMA DE TALES e DEFINIÇAO DE SEMELHANÇA ENTRE TRIANGULOS.Agora ja estou BEM CRCK.
SUGESTAO:gostaria que voces acrescentasse mais perguntas
dificeis.
MAS MESMO ASSIM GOSTEI MUITO.
nov 08, 2007 @ 11:12:20
eu achei o site de vcs é muito bom só que falta algumas perguntas para as pessoas respoinder e depois conferir
mas tudo bem já aprendi bastante com isso!
xau xau
out 31, 2007 @ 15:25:02
deveria ser menor e conter tudo
por q ele tem poucas coisas importantes e é muito grande
out 22, 2007 @ 13:22:55
ñ encontrei o k keria
out 18, 2007 @ 21:41:21
eu gostei pq me ajudou no trabalho de matematica e tirei uma boa nota
out 17, 2007 @ 18:12:14
triângulo equilátero vértice etc
out 05, 2007 @ 16:43:23
leeegal :)
axei tudo que precisava !
set 28, 2007 @ 04:10:36
Gostei pois sou professor de Matematica
set 24, 2007 @ 10:08:50
eu queria q vc espricase mais direito e tbm ensinase melhor as pessoas.
set 22, 2007 @ 11:52:29
posso fazer uma pergunta??
quem sao os redatores desse site??sao profesores de matematica??
gostei muito da forma com a qual eles nos passam a materia..
bjuss
set 22, 2007 @ 11:48:52
Parabens!!!site muito interessante que ta me ajudando demais a estudar pra prova!!adorei site..e seus redatores usam uma linguagem facil e interessante..diferente dos livro.
bjus
set 22, 2007 @ 10:54:19
naum respondeu minhas perguntas e naum sanou minhas duvidas
set 04, 2007 @ 19:13:23
valeu mesmo por ter me ajudado…
???
set 04, 2007 @ 13:02:51
quero os exercicios de teorema de teles
ago 28, 2007 @ 11:02:05
vlw por me ajudar no trabalho!!!!
ago 26, 2007 @ 12:41:40
Gostaria muito de parabenizar este site….Pois ele tem uma ótima explicação….Incarei o mesmo pra todas as minhas amigas!
ago 26, 2007 @ 12:35:45
Achei esse site mto bom….ele explicou tudo que eu precisava saber!
Além de me dar várias informações, me proporcionou vários exemplos!
ago 11, 2007 @ 12:32:00
naum consegui encontrar os exercicios que queria
ago 07, 2007 @ 22:42:25
oi naum gostei muito naum, pois ele fala muito pouco sobre o que queremos saber a respeito sobre tal assunto…
só isso mesmo, o resto esta bom sim.
xau…
jul 17, 2007 @ 21:23:05
mto bom. achei tudo q precisei.
maio 31, 2007 @ 16:18:23
eu adorei.muito bom parabens! rebelde
éso isso tchau! 100%
para todos!
abr 10, 2007 @ 15:08:32
Gostei imenso da explicação, como aluna acho que respondeu ás minhas dúvidas. Obrigada e parabéns
abr 02, 2007 @ 19:46:27
Gostei do material, mas faltou as demostrações de congurencia de triangulos…
abr 02, 2007 @ 14:29:25
nao gostei e uma besteira
mar 22, 2007 @ 15:38:55
mto bom ajuda mto essa explicacao!
mar 15, 2007 @ 22:55:52
O comentário sem dúvida está muito bom, mas é necessário acrescentar alguns exercícios complicados
mar 15, 2007 @ 22:55:50
Como professor de Matemática gostei bastante da maneira como o assunto é abordado e explicado. Está bastante fácil de entender o conteúdo dada a clareza das explicações. Parabéns.
mar 12, 2007 @ 14:59:25
Gostaria de fazer uma pergunta:
No caso de semelhança de triângulos temos na demonstração do Teorema de Pitágoras três triângulos semelhantes. Não consegui identificar qual o critério de semelhança para os triângulos (ABH e AHC) nos quais possuem o lado comum a altura relativa a hipotenusa do triângulo maior ( ABC). Seria o critério LAL, AA ou LLL?
mar 08, 2007 @ 20:00:46
Gostei muito desta materia… minha professora pediu uma pesquisa e havia tudo q ela pediu na respectiva ordem.
Mto bom
fev 23, 2007 @ 11:38:34
gostei muito desse artigo
muito bem explicado
me ajudou pra caramba no trabalho de escola
fev 22, 2007 @ 20:05:17
eu nao entendi nada com essa matéria
fev 11, 2007 @ 16:33:08
Gostei muito desse assunto (congruência de triângulos). Mas gostaria de um assunto mais aprofundado. Se possìvel mandem para o meu email.
Obrigada.
jan 10, 2007 @ 08:32:46
não encontrei os exercícios que queria.
dez 18, 2006 @ 12:21:37
Artigo muito bom. Parabéns. Uma sugestão: publicar um artigo sobre as demonstrações do Teorema de Pitágoras.