Para complementar o artigo escrito sobre Conjuntos Numéricos iremos abordar agora o conceito de intervalo na reta real R. Ou seja, dos subconjuntos de R que satisfazem à seguinte propriedade:
se x e y pertencem a I C R, x ≤ y, então para todo z tal que x ≤ z ≤ y, então z pertence a I
Sem entrar em detalhes, e apenas como informação adicional, a propriedade estabelece que os intervalos são subconjuntos conexos de R, como também o é o próprio R, ou subconjuntos contínuos de R.
Em forma de conjunto a propriedade acima pode ser escrita como:
I = {z ε R | x ≤ z ≤ y}
Os intervalos podem ser classificados por suas características topológicas – abertos, fechados e semi abertos (fechados ou abertos à esquerda ou à direita) – e por suas características métricas – comprimento nulo, finito não nulo ou infinito.
Notação em símbolos de um intervalo
Habitualmente se utilizam os colchetes – “[” e “]” – para indicar que um dos extremos do intervalo é parte deste intervalo e os parênteses – “(” e “)” – ou, também, os colchetes invertidos – “]” e “[” para indicar o contrário.
Assim, por exemplo, dados a e b números reais, com a ≤ b, o intervalo I = (a,b] = ]a,b] representa o conjunto dos x ε R, tal que a < x ≤ b. Note que a não faz parte do intervalo.
Representação de um intervalo na reta real
Um intervalo é representado na reta real utilizando-se de uma pequena “bolinha vazia” para indicar que um dos pontos extremos não pertence ao intervalo e de uma “bolinha cheia” para indicar que o ponto extremo pertence.
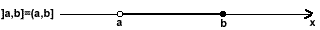
Tipos de Intervalos
Dados a e b números reais, com a ≤ b, x pertencente ao intervalo e c o seu comprimento, podemos classificar os intervalos como:
a) Intervalo Fechado de comprimento finito c = b – a:
[a,b] = {x ε R | a ≤ x ≤ b}
b) Intervalo fechado à esquerda e aberto à direita de comprimento finito c = b – a:
[a,b[ = [a,b) = {x ε R | a ≤ x < b}
c) Intervalo aberto à esquerda e fechado à direita de comprimento finito c = b – a:
(a,b] = ]a,b] = {x ε R | a < x ≤ b}
d) Intervalo aberto de comprimento finito c = b – a:
]a,b[ = (a,b) = {x ε R | a < x < b}
e) Intervalo aberto à direita de comprimento infinito:
]-∞,b[ = (-∞,b) = {x ε R | x < b}
f) Intervalo fechado à direita de comprimento infinito:
]-∞,b] = (-∞,b] = {x ε R | x ≤ b}
g) Intervalo fechado à esquerda de comprimento infinito:
[a,+∞) = [a,+∞[ = {x ε R | a ≤ x}
h) Intervalo aberto à esquerda de comprimento infinito:
]a,+∞[ = (a,+∞) = {x ε R | x > a}
i) Intervalo aberto de comprimento infinito:
]-∞,+∞[ = (-∞,+∞) = R
j) Intervalo fechado de comprimento nulo:
Como o comprimento é nulo e o intervalo fechado, então a = b e esse intervalo corresponde ao conjunto unitário {a}, isto é, a um ponto da reta real.
Concluo a classificação dos intervalos com a seguinte pergunta para vocês: E o intervalo vazio como seria definido?
União e Intersecção de Intervalos
Como intervalos são conjuntos é natural que as operações mencionadas possam ser realizadas. E, trata-se de um procedimento muito comum na resolução de alguns problemas.
E a maneira mais fácil e intuitiva de realizar essas operações é através da representação gráfica dos intervalos envolvidos. Vamos à um exemplo prático de como efetuar tais operações.
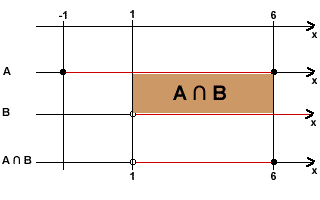
Sejam A = [-1,6] = {x ε R | -1 ≤ x ≤ 6} e B = (1,+∞) = {x ε R | x > 1} dois intervalos e vamos determinar A U B e A ∩ B.
Primeiramente, marcamos todos os pontos que são extremos ou origens dos intervalos em uma mesma reta. Em seguida, abaixo dessa reta, traçamos os intervalos que representam graficamente os conjuntos A e B. E, por fim, é só utilizar a definição de união e intersecção para determinar os trechos que estão em pelo menos um intervalo e os trechos comuns aos dois intervalos, respectivamente. Veja a solução de A ∩ B na figura a seguir e de onde é também facilmente observado o resultado de A U B:
A ∩ B = {x ε R | 1 < x ≤ 6} e A U B = {x ε R | -1 ≤ x}






abr 07, 2011 @ 19:19:37
esse assunto é muito complicado e as vezes não entendo muito bem…
abr 07, 2011 @ 16:39:30
naum,eu detestoo mat,naum sei quase nda mesmo e olha que estou no segundo ano letivo…pra mim é super difiçil entender viu.
mar 29, 2011 @ 10:37:57
Bom gente ! É seguinte intervalos é muito facio e simples ….. basicamente vc vai fazer dessa forma.
[a = bola fechada , ]a = bola aberta , (a = bola aberta (DE QUALQUER FORMA O ( É BOLA ABERTA !)
∞ = ifinito ( seria um oito deitado )
≤ = sempre que tiver isso será bola fechada
(bola-fechada) (bola-fechada)
( NUNCA SE ESQUEÇA DE CONTORNA A RETA COM UMA ESPECIE DE ‘” MATINHO” que seria dessa forma (xxxxxxxxxxxx) [ o x é so um exemplo mas vc tem q riscar a reta
(____________)
B = ________1______3_____________>
(bola-fechada) (bola-aberta)
VlW OBRIGADO ESPERO QUE TENHAM ENTENDIDO
mar 27, 2011 @ 15:31:42
eu não entendi nada , seja mais objetivo
mar 24, 2011 @ 16:59:38
Gente, esse site é péssimo. Sugiro q vocês prestem mais atenção às aulas, ao invés de procurar entender 1 dia antes da prova, como alguns aqui. Intervalos é muito fácil, mas exige um pouco de atenção. E quanto ao infinito, não tem o que errar, seja mais ou menos infinito, a reta estará sempre aberta. Já na união de intervalos, basta somar os extremos, não esquecendo que um deles pode ser infinto.
Brigadão, mas o site é muito ruim…
mar 20, 2011 @ 22:25:30
preciso aprender,tenho prova sobre iso amanhã e estou mal na matéria.
mar 18, 2011 @ 08:21:09
confundiu mais ainda minha cabeça!!!!!!!!!!!!
mar 02, 2011 @ 16:43:38
uhuhuhuhhu foi muito otimo ver esse site obter conhecimentos d
e mat eh fodah muito fodah rsrssrs odeio fazer trabalho de mat por isso eu so pesquiso e depois eh so imprimi carah facil i pratiko…..bjux é nóis na kakuah
fev 25, 2011 @ 16:02:21
não consigo entender esse negócio de intervalos :\ e a prova é amanha, já era
fev 21, 2011 @ 10:26:44
falta os exercícios para resolver.
fev 21, 2011 @ 10:21:41
Gostei bem esta materia mas é préciso dar muitos exercícios sobre os intervalos na recta real.
jan 13, 2011 @ 11:18:59
preciso que me ajudem a resolver ] -00,2]
dez 04, 2010 @ 13:34:35
Gostei mas no meu ver deixa a desejar pois acho incompleta a informação oque me manteve minhas dúvidas por exemplo:
Não podia ser menos infinito na reta demonstrada, oque demonstra nesta reta, que é mais infinito e não menos?
Oque determina a direção da reta de x uma podia ser numa direção e a outra na oposta como ficaria então?
Onde está representado as retas referentes ao sinal de união não tem ?
Falo isso pois comprei vários livros preparatórios para o enem mas pelo que estudei no livro de matemática e suas tecnologias tem muita coisa errada então vim consultar o site de vcs mas minhas dúvidas continuam pois no site de vcs falta explicação mas a iniciativa é ótima . Obrigado mesmo assim.
nov 04, 2010 @ 15:44:57
mt bom´… só acho que deveria ter mais exempolos principalmente sobre comprimento infinito…Valeu…t+
set 20, 2010 @ 23:43:14
Muiito massa véyn
set 14, 2010 @ 11:51:13
preciso aprender estou mal nessa materia
jun 27, 2010 @ 19:39:52
ayaya, gostei muito de aprender intervalos,quando vc presta muito atençao vc sabe fazer é muito legal!!
jun 22, 2010 @ 15:49:10
gostei mt tha bem explicado wleu
maio 29, 2010 @ 18:52:33
muito bom , e interessante tirei minhas duvidas sobre esse assunto……… :D
maio 19, 2010 @ 18:26:57
ACHEI MUITO BACANA;TIROU TODAS AS MINHAS DUVIDAS.
maio 10, 2010 @ 17:50:21
nao entendi nada boiei legal na explicaçao eu só queriacom retas seria mais facil…
maio 05, 2010 @ 10:17:47
Bom dia,
Por favor, podem ajudar-me nessa resolução?
X elevado a 3 = 2.744
Como monto essa equação?
grata
abr 28, 2010 @ 21:03:37
Não achei muito bom, mas do que achei na internet foi o melhorzinho…
abr 26, 2010 @ 12:23:04
quero saber materia sobre conjuntos numerico
abr 25, 2010 @ 21:39:26
Mtoo booaa essa explicaçãao me ajudoou msmoo ‘ ‘—–
abr 23, 2010 @ 19:51:48
Achei muito interessante e muito bem explicado..
so que devia colocar na forma de venn euler
abr 23, 2010 @ 13:03:26
Obrigado, serviu para meu trabalho ! :D
abr 05, 2010 @ 14:25:55
muito legal……….
abr 05, 2010 @ 12:08:22
gostaria que as eplicações fossem em videos
mar 31, 2010 @ 15:52:19
Faltaram os exercícios pra gente fazer né ?!
mar 26, 2010 @ 20:59:24
Para trabalhar essa aula é necesario de um professor do lado.
mar 25, 2010 @ 00:03:02
Muito explicativo, e deu para passar a idéia de forma clara e objetiva. Muito bom!
É, realmente estudar matemática é um saco, gosto muito de física por que tem sempre um propósito direto, mas isso que se aprende no ensino médio em matemática pouquíssimas pessoas vão usar em suas vidas depois de algumas eventuais provas…
mar 14, 2010 @ 19:03:23
Odeioo matematiicaa maiis ee necessario fazer o que !?
taa bem explicadoo gosteii parabeens !
PRODIGIANOOS ! HASUHASUHASUHASUHASUHASUHAS !
mar 13, 2010 @ 20:20:12
Na verdade estava procurando operaçoes com intervalos,gostaria de ter encontrado A-B representado na reta real.
mar 06, 2010 @ 19:54:20
nao entendi
mar 01, 2010 @ 20:46:10
matematica me condena D:
fev 24, 2010 @ 15:37:23
muito interessante. Contribuiu para tirar varias duvidas. Obg !
fev 22, 2010 @ 10:21:53
valeu.gostei
muito da dica sobre união e intersecção de intervalos ajudou bastante.
fev 18, 2010 @ 16:15:08
P0h tava um kaduh facil de intender, se vces explicacem de um m0do mais simples seria melhor
dez 20, 2009 @ 17:26:21
seria mais interessante e ajudaria muito mais se tivesse as esplicaçoes nas retas….
nov 10, 2009 @ 10:14:43
oi muito interessante
set 25, 2009 @ 13:52:50
oi eu n entendi uma coisa quando que eu uso intervalo fechado e aberto e por que vcs n poderiam me explicar?eu to no 1º grau e to com dificuldades para aprender isso vai cai na prova
ago 18, 2009 @ 22:01:54
eu prefiro que isso seja exolicado em uma linguagem mais formal , para que assim possamos assimilar melhor o conteúdo.
ago 16, 2009 @ 14:46:56
Gostei muito, muito bem explicado, mas acho que deveria ter uma liguagem mais simples…
abr 06, 2011 @ 11:27:55
eu tambem adirei saber disso
muito interessante
jul 29, 2009 @ 20:42:47
esplica beem ! mais poderi ater uma linguagem mais facil pra intendermos melhos
jul 17, 2009 @ 08:36:02
rapido, pratico e facil de absorver,aprendi muito com essa explicação
jun 23, 2009 @ 18:36:22
gostei muito de aprender intervalos,quando vc presta muito atençao vc sabe fazer é muito legal
jun 17, 2009 @ 16:13:34
Isso Ai em Cima E MuitO Bom Aprende Muita Coisa!
jun 13, 2009 @ 16:14:56
Odeio MTM :D
maio 25, 2009 @ 15:22:47
ACHEI MUITO INTERESSANTE E CONSEGUI OBTER MUITO MAIS CONHECIMENTO SOBRE ESSE TEMA TAO DISCUTIVEL NA MATEMATICA.