Vamos abordar neste post as propriedades referentes à redução de frações. Alguns conceitos aqui utilizados encontram-se no post Frações – Parte I que podem – e devem – ser consultados em caso de dúvidas.

Redução de Frações

Reduzir uma fração é transformá-la em uma outra equivalente.

Tá legal. Mas o que são frações equivalentes? São aquelas que mantêm a mesma proporção de outra fração, ou seja, é a fração obtida, de uma outra, multiplicando-se ou dividindo-se o seu numerador e o denominador por um mesmo número diferente de zero (veja propriedade 6 da primeira parte).

Exemplo: 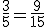. Veja que a segunda fração é obtida a partir da primeira multiplicando-se o seu numerador e seu denominador por 3. Inversamente, a primeira é obtida da segunda dividindo-se o seu numerador e seu denominador, também, por 3.

Os principais procedimentos de redução de frações são:

1. Reduzir inteiros a frações impróprias;
2. Reduzir números mistos a frações impróprias;
3. Extrair inteiros de frações impróprias;
4. Simplificar frações;
5. Reduzir frações ao mesmo denominador.

1. Reduzir inteiros a frações impróprias

Simples. É suficiente multiplicar o número inteiro escolhido por outro número inteiro – de preferência diferente de um – e compor a fração imprópria com o numerador igual ao produto obtido e o denominador igual ao multiplicador – o outro número.

Exemplo. Seja reduzir 7 inteiros a terços:

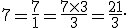
2. Reduzir números mistos a frações impróprias

Para se reduzir um número misto a fração imprópria, multiplica-se a sua parte inteira pelo denominador da parte fracionária e, ao produto adiciona-se o numerador da parte fracionária. Ao total obtido dá-se por denominador o da parte fracionária.

Exemplo. Seja reduzir 5 inteiros e 3/8 (três oitavos) a oitavos.

Como a unidade vale 8 oitavos, 5 unidades valem 5×8 ou 40 oitavos, os quais adicionados aos três oitavos dão 43 oitavos:

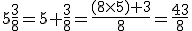
3. Extrair inteiros de frações impróprias

Para se extrair os inteiros de uma fração imprópria, isto é, transformá-la em um número misto, divide-se primeiro o numerador pelo denominador. O quociente dessa divisão representa os inteiros – parte inteira do número misto – e, caso haja resto, este será o numerador da parte fracionária cujo denominador é o da fração original.

Exemplo. Extrair os inteiros da fração imprópria 43/8.

Como a unidade vale 8 oitavos (8/8), temos na fração dada 5 unidades que cabem em 43 (5 x 8 = 40) e sobram 3 oitavos. Em outras palavras, a divisão de 43 por 8 tem como quociente o inteiro 5 e resto 3. Portanto, pela regra, vem;

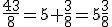
4. Simplificar frações

Simplificar uma fração é reduzir esta fração à uma fração mais simples mantendo-se a proporção da fração original. E o princípio que norteia a simplificação de frações é: uma fração não se altera quando dividimos seus termos por um mesmo número diferente de zero (veja propriedade 6 do artigo anterior).

Observe que para simplificar frações é necessário que haja um divisor comum, além da unidade, aos seus termos. E, torná-la irredutível é obter a fração equivalente em que o único divisor comum aos seus termos é a unidade, ou seja, quando o mdc – máximo divisor comum – entre o numerador e o denominador é igual a 1, o que é o mesmo que os seus dois termos serem primos entre si.

Exemplo. Simplificar a fração 6/18.

Primeiro observe que seus termos são múltiplos de 2. E, portanto, ela pode ser simplificada efetuando-se a divisão de seus termos por 2:

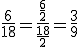
O procedimento acima é, de fato, uma simplificação, uma vez que houve a redução a uma fração mais simples em que a proporção foi mantida. No entanto, ainda não se encontra em sua forma irredutível, pois o 3 é um divisor comum aos termos da fração resultante. Assim, efetuando mais uma simplificação, dividindo-se os termos por 3, vem:

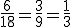
obtendo-se a sua forma irredutível, uma vez que o mdc(3,1) = 1, isto é, 1 e 3 são primos entre si.

Teorema 1. Para reduzir uma fração à sua forma irredutível, é suficiente dividir os seus dois termos pelo seu mdc.

De fato, ao se dividir os dois termos de uma fração pelo seu mdc, obtem-se quocientes primos entre si, e portanto formam uma fração irredutível. Além do mais, essa fração é igual à fração original uma vez que foi obtida dividindo-se seus dois termos por um mesmo número.

No exemplo anterior o mdc(18,6) = 6 = 2 x 3, os fatores utilizados para se determinar a forma irredutível da fração dada. O mesmo resultado, claro, seria obtido se efetuassemos a divisão por 6.

5. Reduzir frações ao mesmo denominador

Reduzir frações ao mesmo denominador é determinar frações equivalentes às frações dadas e que tenham o mesmo denominador.

Novamente, o princípio em que se baseia a redução de frações ao mesmo denominador é o estabelecido na propriedade 6 do artigo anterior: Uma fração não se altera quando os seus dois termos são multiplicados pelo mesmo número diferente de zero.

Regra 1. A regra mais simples de se reduzir várias frações ao mesmo denominador é multiplicar os dois termos de cada uma pelo produto dos denominadores de todas as outras.

Exemplo 1. Reduzir ao mesmo denominador as frações 3/5 e 6/7.

Aplicando a regra 1, vem:

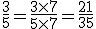e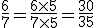

Como você é esperto deve ter notado que as frações obtidas são equivalentes às primitivas, pois resultaram da propriedade acima apontada e têm o mesmo denominador, igual ao produto dos denominadores das frações originais.

Exemplo 2. Reduzir ao mesmo denominador as frações 1/2, 2/3, 3/4.

Pela regra 1:

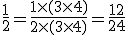
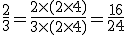
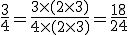
Regra 2. Redução de frações ao mesmo denominador comum utilizando-se o mmc (mínimo múltiplo comum). Pela própria definição de mmc o denominador assim obtido será o menor denominador comum das frações equivalentes, o que só ocorrerá pela regra 1 se os denominadores das frações dadas forem primos entre si. Passos:

• Simplificar as frações (não necessário, mas recomendado, pois facilita os cálculos);
• Determinar o mmc dos denominadores das frações originais ou simplificadas. Este será o denominador comum das frações equivalentes;
• Multiplicar o numerador de cada fração pelo quociente entre o mmc e o denominador desta fração. Este procedimento determina o numerador das frações equivalentes.

Exemplo. Reduzir ao mesmo denominador as frações do exemplo 2 da regra 1.

Primeiro passo: não se faz necessário pois todas as frações estão na forma irredutível.

Segundo passo: O mmc(2,3,4) = 12. Este será o denominador comum.

Terceiro passo: N1 = (12/2)x1 = 6; N2 = (12/3)x2 = 8; N3 = (12/4)x3 = 9, onde N1, N2 e N3 são os numeradores das frações equivalentes.

Logo as frações equivalentes são: 6/12; 8/12 e 9/12.

Referências:

Elementos de Aritmética, Curso Superior – Para o curso colegial e admissão às escolas superiores, do Irmão Isidoro Dumont, Coleção de Livros Didáticos F. T. D, publicado em 26/10/1945