No quarto número do Exercícios Resolvidos vamos colocar em prática a teoria apresentada no artigo sobre Logaritmo, o qual, sugiro, você deve consultar em caso de dúvidas, uma vez que serão apenas mencionadas as propriedades ali abordadas.
Exercício 1: Se logaba = 4, calcule:
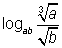
Solução:
Reescrevendo a expressão com o uso das propriedades dos logaritmos indicadas abaixo do sinal de igualdade, temos que:
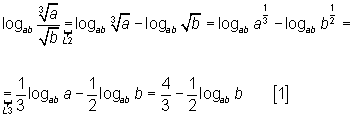
Por outro lado, da condição inicial do exercício e da definição de logaritmo vem:
logaba = 4 => a = (ab)4 => a = a4b4 => b4 = 1/a3 => b = (1/a3)1/4 = 1/a3/4
Observe que acima foi considerado, apenas, o valor real de b maior do que zero na extração da raiz de índice 4 (condição de existência do logaritmo)
Substituindo o valor de b em logabb na expressão [1]:
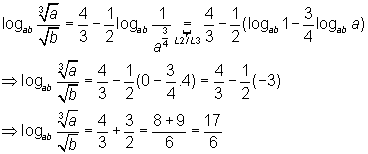
Exercício 2: Se a, b e c são reais positivos com a diferente de 1 e ac diferente de 1, prove que:
logab = logacb(1 + logac)
Solução:
Note que a expressão do lado direito da igualdade possui um logaritmo na base ac. Assim, nada mais natural do que efetuarmos, incialmente, a mudança para essa base (L4) na expressão do lado esquerdo da igualdade. Assim:
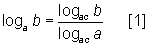
Por raciocínio semelhante ao anterior, fazendo a mudança de base no denominador da fração para a base a, obtemos:
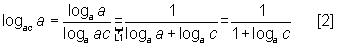
E, substituindo [2] em [1]:
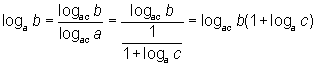
Exercício 3: Se a e b são raízes da equação x2 – px + q = 0 (p, q > 0 e q diferente de 1), demonstre que:
logqaa + logqbb + logqab + logqba = p
Solução:
Aplicando a propriedade L3 ao primeiro membro da igualdade (definimos como A) vem:
A = alogqa + blogqb + blogqa + alogqb
Colocando os termos comuns em evidência:
A = (a + b)logqa + (a + b) logqb => A = (a + b)( logqa + logqb)
E, pela propriedade L1:
A = (a + b) logqab [1]
Como todos vocês sabem (espero) que em uma equação do segundo grau mx2 + nx + k = 0 a soma e o produto de suas raízes valem, respectivamente:
S = -n/m e P = k/m
vem, pelas condições iniciais do exercício, que:
a + b = p e a.b = q
Substituindo esses valores em [1]:
A = plogqq = p
Exercício 4: Se a, b e c são as medidas dos lados de um triângulo retângulo de hipotenusa de medida a e sabendo que a – b e a + b são diferentes de 1, demonstre que:
loga+bc + loga-bc = 2loga+bc.loga-bc
Solução:
Como o triângulo é retângulo, pelo Teorema de Pitágoras:
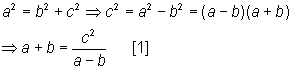
Efetuando a mudança de base (de a + b para a – b) da primeira parcela:
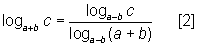
E substituindo no primeiro membro da igualdade a ser demonstrada:
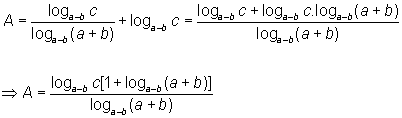
E, por fim, de [1] e [2] vem que:
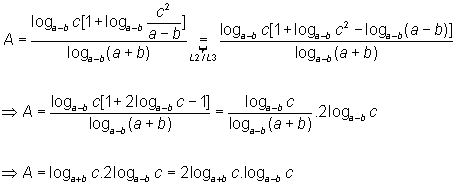
Exercício 5: Demonstrar que:
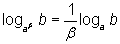
Solução:
A demonstração é consequência da propriedade L4 (mudança de base):
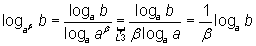
O exercício foi incluído, apesar de simples, por não ter sido tratado nas consequências da propriedade L4 do artigo sobre Logaritmo.
Exercício 6: Se a, b e c são reais positivos e diferentes de um e a = b.c, prove que:
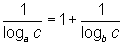
Solução:
Pela propriedade L4 (mudança de base) temos:
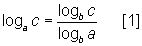
Da condição inicial, aplicando-se o logaritmo na base b, obtemos:
logba = logbbc = logbb + logbc = 1 + logbc [2]
Substituindo [2] em [1]:
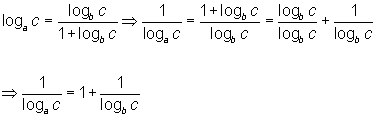
Referência:
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.





abr 09, 2008 @ 21:13:49
parabens pela atitude
abr 08, 2008 @ 18:43:25
cada dia que passa me sinto mas ferrada porque quando mais eu procuro saber sobre logaritmos mais perdida eu fico preciso de ajuda ….sttephaniemedeiros@hotmail.com por favor quem quizer ajudar agradeço desde ja
abr 01, 2008 @ 19:21:43
eu estou muito com muita dificuldade com as funções trigonometrica
mar 26, 2008 @ 10:56:19
envim-me exercicios resolvidos
mar 18, 2008 @ 20:03:35
eu adorei esse site vei na moral me ajudou muito em umas questoes aqui vou pesquisar aqui direto valew ai.
mar 10, 2008 @ 12:49:31
gostaria que voçes colocacem exemplos mais faceis tipo:
log x=4/3
²
log 8=2
x
log(2x-1)=1/2
²
log log log 64
¹ ³ ²
se voçes puderem resolver esses exercícios eu agradesso
brigadão e me ajudem!!!
mar 08, 2008 @ 16:44:04
é muitoo boom saber que podemos ter essa ajuda pela net!!!!
mas eu tenho uma questão que eu não consegui resolver e nem entender.é assim: calcular pela definição de x:
a)log3 log2 x = 0
será que vocês poderiam me ajudar???
agradeçooo desde já!!!!
jan 28, 2008 @ 08:48:38
bom
10
fui
jan 02, 2008 @ 17:10:34
Gostaria muito de obter ajuda para a resolução de uma questões envolvendo multiplicação de matrizes sendo matrizes A 2×2 e B 2×3,
Desde já muito obrigada.
dez 13, 2007 @ 17:38:26
gostei das resoluçoes, mas vcs deveriam incluir exercicios envolvendo problema de raciocinio logico
dez 01, 2007 @ 01:27:07
gostaria que me ajudasse a resolver a seguinte questão:
Qual o número de soluções da equação
x
2 – 4 = log (x + 4)
2
(leia: 2 elevado a x menos 4 igual a logaritmo de (x – 4) )
Desde já agradeço!
Rosânia
nov 30, 2007 @ 23:47:32
Nossa q osso!!!
to comessando a relembra as propriedads de log =/
nov 30, 2007 @ 16:16:36
DEIXE EXEMPLOS COM NUMEROS!
nov 30, 2007 @ 11:54:43
Gente me envia por e-mail loocknys@hotmail.com 150 execícios resolvidos de sistema linear.
nov 26, 2007 @ 20:40:02
queria exercicios resolvidos de trigonometria por favor me ajudem
nov 24, 2007 @ 14:06:33
Adorei o site…
muito obrigado por colocar esse site na internet…
exercicios muito bm resolvidos i explicados…
obrigado mesmo…
adeus
nov 08, 2007 @ 01:43:01
MEDOOO
out 26, 2007 @ 13:00:26
foi a 1ª vez que navegei novosso site e gostei muito
out 22, 2007 @ 19:21:01
Gostaria que vocês botassem exerc´cios com números e questões de vestibulares…
out 15, 2007 @ 15:47:15
Este saite e muito bom , mais ainda nao exclareci as minhas duvidas…
out 11, 2007 @ 21:11:55
presiso de ajuda gente!!!
1) Um caminhão cujo peso vazio é 3000 Kg será carregado com 480 caixas de 10 Kg cada,
1 ) 350 caixas de 8 Kg cada, 500 caixas de 4 Kg cada e 800 caixas de 5Kg cada. O motorista
do caminhão pesa 80 Kg e a lona de cobertura da carga pesa 50 Kg.
a) Se este caminhão tem que passar por uma balança que só permite passagens a caminhões
com peso máximo de 15 toneladas, este caminhão passará pela balança?
b) Qual o peso médio das caixas carregadas no caminhão?
2)Um produto é vendido em três supermercados por $130/KG, $132/Kg e $135/Kg. Determine
, em média quantos quilos do produto se compra com $1,00.
out 11, 2007 @ 15:11:09
em uma pesquisa, apos N messes da constatacao da existencia de uma epidemia, o numero de pessoas por ela atigidas era F(N)= 40 000
………..-2 nesse tempo a ipdemia atinge pelo menos 4.000
2+15.4 de pessoas e de aproximadamente? LOG:2= 0.3 E LOG 3=0.48 (BOM SE ALGUEM CONSIGUI RESOLEVA ESE PROBLEMA ENVIE PARA MEU EMAIL hellen_pba@hotmail.com PRESISO MUITO DESSA RESOLUÇAO OBRIGADU
out 05, 2007 @ 09:20:15
essa matéria irá me ajudar muito a escapar da reprovação
já que estamos em final de ano!!!
set 27, 2007 @ 18:26:49
seja a funcao f;R R defna por f(x)=3expoente x.determine os valores de x e ER,tais que f(x+1)+f(-x+4)=36.quero saber como calcular.
set 25, 2007 @ 16:13:57
Eu odeio Matematica, nunka consigu fazer nada, principalmente em provas, gostei mto desse site pq tdas as minhas duvidas sumiram.
set 20, 2007 @ 22:43:53
quero0 aprender geometria ainda não aprendi mais é bom
set 13, 2007 @ 13:56:26
para benes por este conceito
set 10, 2007 @ 14:26:24
LOG3 (2x+1) – log3 (5x-3) = -1 ???
gostaria de saber a resolução desta equação..
ago 21, 2007 @ 11:47:00
Esse site é nota 10000!!!! Gostaria que vcs me mandassem exercícios resolvidos sobre PA cujos termos são logs. Obrigado.
ago 13, 2007 @ 21:42:50
ai manos sem palavras!!!!!esse site é nota 1000!!!!!tive um pouco de dificuldades na questão 2.Mais ai,tirando isso valeu mesmo e um grande abrços a toda garela que curte à matemática, e um fote abraços ao grande e saldoso Gelson Iezzi.valeu,fui.
jul 22, 2007 @ 12:49:31
o exemplo que tem da pra tirar algumas duvidas minha em relação ao assunto queria que tivese mas exemplo com log na mudança de base
jun 19, 2007 @ 20:04:33
iaiiiiii galera da matematica,blz a todos po eu tou tranquilo ai quero llhe dar os parabens aqueles que fizeram alguns exemplo d logaritmo,po valeu mesmo eu amo matematica so sou meio cabeça dura quase n entendi nada,mais ai valew mesmo um abraçao a todos.
jun 17, 2007 @ 18:50:52
é bom saber que a qualquer hora ao resolver logaritimos, tenho ajudas dos mais experientes na matéria. so me arrependo por vos ter encontrado tarde, ate porque, sou apaixonado por matematica. todos voces sao mui xpecial pra mim e pra o meu futuro. obrigado e sucessos espero que continuem assim!!!!!!!!!!!!!!!!!!
jun 13, 2007 @ 22:30:45
questoes bem interessantes, passamos muito tempo respondendo, valeu….
jun 13, 2007 @ 22:03:36
quero questoes mais dificeisl, que estas esta tão facil
jun 13, 2007 @ 21:30:59
Prezados,
Tenho dois exercícios sobre estatística/probabilidade e não consigo resolvê-los, alguém pode ajudar?
1) O tempo necessário, em uma oficina, para o conserto de transmissão para certo carro é normalmente distribuído com média 45 min e desvio-padrão 8 min. O mecânico planeja começar o conserto do carro 10 min após o cliente deixá-lo na oficina, comunicando que o carro estará pronto em 1 h. Qual a probabilidade de que o cliente tenha que esperar caso o mecânico esteja enganado?
2)Nos últimos anos, as empresas de cartões de crédito intensificam esforços no sentido de abrir mais contas para alunos de faculdade. Suponha que uma amostra de 200 alunos em uma faculdade apresentou as seguintes informações em termos do aluno possuir cartão de crédito bancário e/ou cartão de crédito de viagem e entretenimento:
CC de viagem e entretenimento
Sim Não Totais
Sim 60 60 120
CC bancário Não 15 65 80
Totais 75 125 200
(a) Se um aluno é selecionado aleatoriamente, qual a probabilidade de que o aluno possua um cartão de crédito bancário?
(d) Se um aluno é selecionado aleatoriamente, qual a probabilidade de que o aluno não possua um cartão de crédito bancário nem cartão de viagem e entretenimento?
(h) Os dois eventos, possuir um cartão de crédito bancário e possuir um cartão de viagem e entretenimento, são estatisticamente independentes? Explique.
jun 13, 2007 @ 16:40:56
Parabenizo pela iniciativa, gostaria de pedir uma ajuda.
Eu nunca vi esse assunto (Logaritmo) e tenho q apresentar um sminário sexta-feira agora.
Tem como alguém mandar algum material falando sobre?
Mobral mesmo.
Valeu…
jun 12, 2007 @ 17:41:41
cosegui resolver os exercicos me a judou muito valeu!! esse site é
10*10=?
R=100
maio 28, 2007 @ 11:51:49
muito bom,mas deveria ter assim:log2(12-2x)=2x
maio 02, 2007 @ 15:48:07
parabens foi com a ajuda do seu site que passei em meu primeiro concurso o trabalho deb vcs é super importantissimo
que leu essa mensagem por favor siga o que eu falei que vcs nao vao se decepcionar
maio 01, 2007 @ 16:15:34
O trabalho de vocês é importantíssimo para quem precisa preparar-se para concursos.Parabéns e muito obrigado.
abr 05, 2007 @ 18:33:45
se tenho uma potencia na qual o expoente é muito grande qual á regra para sabermos o valor desta potencia. ficarei muito grato se responder-me.
mar 17, 2007 @ 14:34:52
Eu gostaria de ver tb soluções de função exponencial
jan 13, 2007 @ 22:51:13
Vcs foram bem legais ao colocar esses exercicios esplicativos pois assim podemos estudar com uma base maior
Obrigada tb pelo espaço cedido a nós pra nos manfestar e falar o que nós achamos desse site
jan 13, 2007 @ 22:49:02
è bem legal poder contar com essa ajuda da net sempre!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
nov 16, 2006 @ 10:01:23
to com uma duvida com relaçao a dus questões sobre log e gostaria que vcs me ajudassem: a primeira é: 0,1 elevado a 2x = 0,24 em R
considere log de 2 = 0,3 e log de 3 =0,48. qual a soluç~ao da equação?
A segunda é: um certo capital é aplicado em regime dem juros compostos a uma taxa anual de 12%. depois de quanto tempo esse capital será triplicado?
grato!
out 01, 2006 @ 17:23:58
Desejaria que vces podessem enviar novidades de novos exercícios resolvidos de matemática com os seguintes assuntos: geometria plana, geometria espacial, matrizes, PA e PG, probabilidades, trigonometria e analise combinatória.
Grato pela atenção.
Jefferson.
set 19, 2006 @ 11:09:14
Fala chefe…
Esse artigo me ajudou muito pra prova de teoria da codificação hoje…
Fica na Paz….
set 18, 2006 @ 19:35:43
Não gostei voces não tirou minhas duvidas…
set 10, 2006 @ 11:11:46
o vosso trabalho è muito bom .Parabèns