Dentro do mesmo princípio adotado no post Passe de Mágica, em que muitas pessoas conhecem o fato, e o assumem como verdadeiro com uma naturalidade surpreendente, mas não o porquê do fato, dissertarei sobre conceitos e principais propriedades da potenciação visando demonstrar que a0 = 1, para a diferente de zero, muito embora não tenha significado como operação, em vista da definição de potenciação dada abaixo. Como se verá trata-se, como no caso do post mencionado acima, de uma demonstração muito simples (ou trivial no linguajar matemático).
I. DEFINIÇÕES
Vamos começar do começo – eita que frase arretada! – definindo, de maneira simples e direta, que potenciação de um número relativo a nada mais é do que a multiplicação reiterada de a por ele mesmo um número n de vezes, n inteiro e positivo. Ou seja:
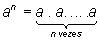
onde se estabeleceu a notação (ou representação simbólica) an para indicar de forma resumida e simplificada (e, diga-se, criativa) esse produto, denominando-se a a base da potência e n o expoente ou grau da potência. Se lê a representação simbólica an como “potência n de a” ou “potência enésima de a” ou “a elevado a n“.
Potência de grau n de a é o produto de n fatores iguais a a. Assim:
- a0 é a potência de grau zero de a ou potência de expoente zero, a um número real diferente de zero;
- a1 é a potência de grau 1 de a, sendo igual ao próprio a. Neste caso é dispensável escrever o expoente;
- a2 é a potência de grau 2 de a, conhecida como quadrado de a ou a ao quadrado;
- a3 é a potência de grau 3 de a, conhecida como o cubo de a ou a ao cubo.
II. PROPRIEDADES DA POTENCIAÇÃO
a) A potência de grau n de um produto é igual ao produto das potências de grau n dos fatores deste produto. Ou seja:
[1] (abc)n = an.bn.cn [2]
A recíproca também é verdadeira.
Antes de apresentar a demonstração vale explicitar o que significa recíproca. Tomando a igualdade acima, a justificação da propriedade deve ser feita partindo-se de [1] para obter [2]. A recíproca (como o próprio nome diz) é feita partindo-se de [2] para obter [1].
Demonstração:[1] -> [2]
Por definição:
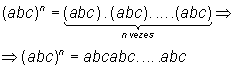
Como a ordem dos fatores de um produto não altera o produto, temos:
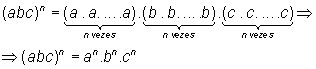
Reciprocamente ([2] -> [1]):
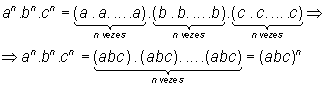
b) O produto de potências de uma mesma base é igual à potência desta base, cujo expoente é a soma dos expoentes dos fatores:
am.an = am+n
Em outras palavras, em um produto de potências com a mesma base, conserva-se a base e soma-se os expoentes. A recíproca é verdadeira.
Demonstração:
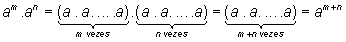
A recíproca deixo por conta do leitor.
c) O quociente de potências de um mesma base é igual à potência desta base, cujo expoente é a diferença entre os expoentes do dividendo e do divisor; isto é:
Em outras palavras, em um quociente de potências com a mesma base, conserva-se a base e subtrai-se os expoentes. A recíproca é verdadeira.
Demonstração:
Suponhamos que m > n. Então:

Eliminando o fator comum ao dividendo e divisor [(a.a … a) n vezes], obtemos:
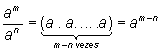
A demonstração da recíproca é fácil, como o de resto, e fica para o leitor se exercitar.
d) A potência n da potência m de um número relativo a é igual a potência de a cujo expoente é o produto dos expoentes m e n, ou seja:
A recíproca é verdadeira.
Se você chegou até aqui, obrigado pelo interesse. Em vez da demonstração aproveito para colocar algumas considerações:Matemática se aprende com o entendimento dos seus conceitos, de saber interpretar as questões, dos porquês da verdade de cada assertiva (as demonstrações) e, principalmente, muita transpiração. Por isso pratique e pratique, pois sómente assim você desenvolve melhor sua capacidade de raciocínio para solucionar problemas e fixar os conceitos.
É com este espírito que deixo como exercício a demonstração desta propriedade. Caso tenha dificuldades entre em contato ou deixe seu comentário. Estarei por aqui pronto para atendê-lo.
e) Potência de expoente negativo de um número relativo a diferente de 0:
A recíproca é verdadeira.
Demonstração:
Antes de demonstrar esta propriedade, farei a demonstração do fato que originou este artigo, i.é, a0 = 1, a diferente de zero. Vamos lá.
Por um lado temos que am/am = 1. E por outro, pela propriedade c) que am/am = am-m = a0 => a0 = 1. Trivial, não.
Agora, fica mais fácil demonstar a propriedade. Primeiro:
a-m = a0-m
Pela propriedade c:
a-m = a0/am = 1/am c.q.d. (como queríamos demonstrar).
A recíproca, mais uma vez deixo como exercício.
E, finalmente, sem entrar no mérito, apresento algumas regras de como proceder com o cálculo de potências em que a base é um número negativo.
- Se o expoente é par, o resultado é positivo;
- Se o expoente é ímpar, o resultado é negativo.
Faça seus comentários. Apresente sugestões e na medida do possível procurarei lhe atender.
[ATUALIZAÇÃO] 26/03/2006: Veja o artigo publicado sobre radiciação. [ATUALIZAÇÃO] 24/04/2006: Veja o artigo publicado sobre Equações Exponenciais.Referência: Abecedário de Álgebra de Darcy Leal de Menezes.
Recomendo fortemente a leitura do artigo Dificuldades para aprender Matemática, publicado no site Tecnociência por Domingos Verena.





set 11, 2010 @ 20:33:24
o site é muito bom, porém, poderia ser utilizada uma forma de escrita mais clara, pois as resoluções são simples, mais acabam se tornando difíceis pelo modo em que são escritas…mais…agradeço…pois me ajudou mto….
parabens
ago 04, 2010 @ 10:15:39
olha so que interesante
estou aprendendo isso
la na minha escola
isso è muito bom
porque a pessoa ]aprende muito mais!!!
by;kait
jul 23, 2010 @ 12:32:16
Gostaria de saber,como resolver esta questão: como escever os numeros a sequir como uma adição de potencia.
os numeros são 56, 154 e 385
.
jul 19, 2010 @ 16:44:47
gostei muitoooo desse saite!!!!!! obrigada por tudo!!!
jul 15, 2010 @ 10:51:34
eu nao sei de nada disso eu só sei rais quadrada, mmc, mdc e radiciação
jul 13, 2010 @ 12:03:11
A EXPLICAÇÃO É VÁLIDA, PENA QUE O LINGUAJAR TÉCNICO( TERMO TÉCNICO)
SEJA DE POUCA UTILIDADE PARA AS PESSOAS QUE REALMENTE QUEREM APRENDER COM RAPIDEZ E CLAREZA. DOMINAR UM ASSUNTO É DIFERENTE DE ENSINÁ-LO. PARA QUE ESTE SITE SEJA MAIS ÚTIL, ACONSELHO UMA FORMA DE EXPLICAÇÃO MAIS CLARA E OBJETIVA.
GRATO.
jun 30, 2010 @ 14:35:04
como resolver esta potencia. 1+10+10²+10³+…10 elevado a2004+ 10 elevado a 2005+10elevado a 6
maio 06, 2010 @ 20:27:07
pq a matematiicaa euma materiaa q neii toodoo mundoo gostaaa????????
maio 06, 2010 @ 20:24:20
porque na potência o numeral 3 se ler:ao cubo?
maio 06, 2010 @ 10:00:37
gostei muito desse site, vou sempre visitar ele
vlw msm….xauu!!!
abr 22, 2010 @ 16:38:42
eu gostei muito desa potenciação ela e muito boa pra quem nao sabe temos que estuda muito para ter nosso futuro na vida
abr 20, 2010 @ 11:33:22
muito bom nota 10 para esse site muito bom mesmo aquoraeu so pesquiso aqui.
abr 12, 2010 @ 09:44:32
muito bom essas contas tirei nota 10!!!!
abr 06, 2010 @ 20:30:22
quero ajuda para resolver o seguinte poblema de potencia. um biologo obsevou o crescimento de uma planta aguatica e presebeu que a cada 2 meses o diametro da planta duplicava.sabendo que a inicio das obsevaçoes o diametro da planta era igual a1 centimetro,qual sera o diametro da planta ao fim de 1 ano?(me ajude a resolver este poblema)
mar 23, 2010 @ 20:54:14
quero muito saber como surgiu a potência matemática para hoje obrigada
mar 20, 2010 @ 17:42:12
tô desesperada… Preciso saber quem inventou a potenciação(pra ontem), tenho trabalho da faculdade, já procurei em muitos sites, não consigo achar… Já vi Pitágoras, René Descartes, mais não tenho provas ! Me ajudaaaaaa ?!
mar 15, 2010 @ 17:04:49
muito ruim vcs deviam aprofundarmais o assunto
fev 27, 2010 @ 07:48:40
Parabens pela explicação
fev 25, 2010 @ 00:39:27
Euu queriiaa todos os 13 propriedades das potencias?Tem como passa pra mim pro favor.
Obriigada
jan 07, 2010 @ 15:27:48
Eu posso na adição de potencias de mesma base , conservar a base e subtrair 1 do expoente?
por favor este exercicio caiu em uma prova e eu não soube responder
A média aritmética entre 9 elevado a 10 e raiz quadrada de 3 elevado a 40 e 6 elevado a vinte.
alguem pode me ajudar?
out 08, 2009 @ 19:27:00
noosaaa vaaleeu :D
out 08, 2009 @ 15:14:41
Adorei esse site
só tenho que agradeçer a vcs!!!
bjs!!!
set 19, 2009 @ 13:40:20
Gostaria de saber como resolver a questão abaixo.Sabendo que a resposta é 2.
2^3^2^1^8^7^6/4^2^2^8^0^9^6
Agradeço desde já.
[°g°]
set 16, 2009 @ 14:03:42
Favoritei… ótima explicação…
[]´s e parabéns
set 02, 2009 @ 02:05:19
pow eu nunca vi feras da matematica
elesarrebenta
ago 14, 2009 @ 20:35:12
adorei esse site obg pela ajuda
ago 04, 2009 @ 11:36:25
como se resolve:
a b c
300=2 .3 .5
a+b+c?
jul 30, 2009 @ 07:23:39
yá, gostei do conteúdo e até extáí matéria para acrescentar nas que já tenho de formas a enriquecer o que já tenho, yá é isso.
jul 25, 2009 @ 18:20:57
esse site é realmente muito util, gostaria de saber como se resolve:
4/3 4/3 1/2
( a + b )
agradeço a ajuda
jul 06, 2009 @ 23:22:46
Gostaria de saber como resolvo 200.000, dividido por (1,04) elevado a 24? 200.000/(1,04)^24 na mão, sem calculadora.
Aguardo resposta ansiosa..rsr. Muito obrigada.
jul 05, 2009 @ 15:44:32
qual a regra para esta operação? y2+y3 (soma de base igual e expoente diferente)
jun 15, 2009 @ 18:01:41
Pretendo encerir as potenciacao no meu tema do fim docurso de formas consigo exactamente dentro desta sugestao possa ter uma ideia sobre a materia.
jun 10, 2009 @ 19:26:53
eu sou da 6º serie e vim pesquisar potenciação por que vc estão ensinando coisa que não eu ainda não aprendi é assim que eu aprendi:
-(-3)
ve se ensina corretamente!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Valeu
ass:Vitor Bueno
jun 10, 2009 @ 15:50:19
Adorei a explicação, faço o curso de matemática na UFSM, e na cadeira de algebra, especialmente, temos que demonstrar tudo. E aqui tudo está muito claro. PERFECT
maio 27, 2009 @ 19:23:52
porque na potência o numeral 3 se ler:ao cubo?
maio 08, 2009 @ 16:07:35
como eu faço para descobrir o numero de algarismos de uma multiplicação de duas notações cientificas?????????????
maio 08, 2009 @ 10:02:38
Não arrisque e nem entre nesse site
maio 07, 2009 @ 13:29:00
Eu nao sabia o que era potênciação bem meu professor vai ficar muito feliz em saber que eu pesquisei sobre ”MATEMÁTICA” pretendo me evoluiir esses assuntos pretendo mais nessas coisas de matematica pra falar verdade tô gostando muito mesmo bj: WalkiriaLeal
orkut : http://www.orkut.com.br/Main#Profile.aspx?rl=mp&uid=14378221591130991184
maio 06, 2009 @ 16:59:32
SOLICITO SE ALGÉM PODE RESOLVER A SEGUINTE QUESTÃO:
100 120
2 – 1 x 2 – 1
abr 28, 2009 @ 15:59:36
bom,não sabia que potênciação é tão importante?? mas eu sei que a minha professora de matemática vai amar se souber que eu pesquisei a potênciação pos eu aposto que ninguemsoube pesquisar…
aprendi muito com esse site!!
ass:Raysa Odwyer
abr 28, 2009 @ 14:21:24
olha ficou otimo o meu
dever mas eu ñ entendo muito essa coisa ñ
abr 14, 2009 @ 12:37:16
AMEI ! ♥
Meu professor de matematica é MUITO BOM .. mas já chegou o dia da prova e eu ainda estava com algumas dúvidas ! Me esclareceu todas …
OBRIGADO !
abr 07, 2009 @ 16:48:08
gostaria de saber a origem da potencia e da raiz se puderem me ajudar eu peço que me mande o mais rapido possivel
abr 06, 2009 @ 22:28:36
eu queria saber a origem da potencia e da raiz (quem inventou,onde surgiu essas coisas)se puderem me ajudar eu agradeço muito.
abr 02, 2009 @ 10:44:52
ñ gostei muito pq a materia ta muito dificil e eu sou da 5 serie!!!+ quem ta elevada esta bom!!!!!!!!!!!!!!!
mar 30, 2009 @ 21:26:40
bligada mi ajudo bastãtão!!!!!!!!!!!!!!!!!!!!!!!!!!!!
mar 29, 2009 @ 14:41:21
como resolvo o problema q é
6 elevado a 6ª + 6 elevado a 6ª+ 6 elevado a 6ª + 6 elevado a 6ª + 6 elevado a 6ª + 6 elevado a 6ª ?
no meu livro a resposta está 6 elevado a 7ª , como chegou a esse resultado, por que eu pensei que fosse 6 elevado a 36ª !
mar 25, 2009 @ 17:22:04
Quanto a questao da Roseli, o resultado é 1.
Se entendi a pergunta, 2exp-2 . 16exp-2 / 4exp-5
fica 2exp-2 . (2exp4)exp-2 . (2exp2)exp5
em seguida:
2exp-2 . 2exp-8 . 2exp10 = 2exp (-2-8+10) = 2exp0 = 1
mar 25, 2009 @ 10:36:53
Como faço para resolver a seguinte questão: Escreva o resultado das expressões na forma de uma potencia::
a)16 . 8 elevado a três . 64 elevado a dois
b)81 . 9 elevado a três : (3 elevado a cinco)2
mar 17, 2009 @ 12:07:12
Site muito bom, muitos questões que foram dadas em aula , acabei tendo maior esclarecimento pelo site,
Só que não consegui resolver uma questão:
como faço para calcular base 2 expoente -2 . 16 com exp.-2 dividido pela base 4 com expoente -5 ???????????
refiz várias vezes e não consegui chegar ao resultado.
abraços