Radiciação
março 25th, 2006
INTRODUÇÃO
No artigo publicado em 23 de fevereiro de 2006, aqui no VICHE, abordei a definição e propriedades da potenciação. Caso você não tenha o domínio desse assunto, sugiro a sua leitura, visando uma melhor compreensão do que será exposto a seguir. O interesse demonstrado pelo tema foi e ainda permanece considerável, tomando-se por base o número de visitas ao artigo (1030 até o momento em que escrevia este post, segundo dado estatístico fornecido pelo software Webalizer). Agora, dando continuidade, trataremos da radiciação de números relativos e expressões algébricas.
Serão tratados os conceitos e propriedades da radiciação sob o ponto de vista primordialmente teórico, como no da potenciação, acrescidos de alguns exemplos. No entanto, caso seja demonstrado interesse, estarei criando uma seção específica (aceito sugestões para o seu nome) com o objetivo de responder, com o devido detalhamento, a questões e dúvidas colocadas nos comentários ou enviadas para o E-Mail nghorta@brturbo.com.br. As soluções serão fornecidas dentro do mesmo padrão aqui adotado, uma vez que é praticamente inviável de serem apresentadas diretamente no formulário dos comentários, devido às restrições ali impostas.
Apenas uma ressalva: por limitação de tempo, pois tenho que ganhar o pão nosso de cada dia, do trabalho que dar escrever artigos de matemática (estou “matutando” escrever um post sobre este fato) e em função da demanda, talvez não tenha condições de responder a todas as dúvidas e questões. Porém, prometo fazer todo o esforço necessário para não deixar nenhuma de fora. Por último, solicito que as questões sejam elaboradas da forma mais clara possível e se reportem, preferencialmente, ao assunto que está sendo tratado – no caso radiciação.
DEFINIÇÃO
Radiciação de números relativos é a operação inversa da potenciação. Ou seja,
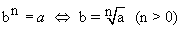
Em outros termos, dado um número relativo a denominado radicando e dado um número inteiro positivo n denominado índice da raiz, é possível determinar outro número relativo b, denominado raiz enésima de a (ou raiz de índice n de a), representada pelo símbolo 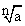, tal que b elevado a n seja igual a a.
Antes de partir para o próximo tópico – as propriedades da radiciação – algumas observações importantes e exemplos:
- O símbolo <=> indicado na fórmula acima significa se e sómente se. Isto é, se a expressão antes desse símbolo é verdadeira então a segunda também é, e vice-versa;.
- Na definição acima, temos que bn = a. Substituindo o valor de b (segunda igualdade), obtemos que
, i.e., a potência de grau n da raiz enésima de a é igual a a;
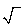é o símbolo de raiz ou sinal de raiz ou simplesmente radical;
- Radical, além de ser o símbolo acima indicado, é também, por extensão, a raiz de um número relativo ou de uma expressão algébrica;
- Raiz de índice 1 (n = 1) de a é o próprio número a;
- Raiz de índice 2 (n = 2) de a é denominada de raiz quadrada de a. Neste caso não é necessário escrever o índice n no radical;
- Raiz de índice 3 (n = 3) de a é denominada de raiz cúbica de a;
- Extração da raiz enésima de a é o cálculo dessa raiz;
- O valor da raiz enésima de a nem sempre é um número racional (inteiro ou fracionário), uma vez que nem sempre a é uma potência de grau n, n inteiro, de b (por exemplo: raiz quadrada de 2);
- Mesmo nesses casos é possível representar a raiz como uma potência de expoente fracionário (detalhes serão fornecidos mais a frente), embora sem significado como operação (exemplo: a raiz quadrada de 2 é expressa como 21/2);
- Erro de aproximação, é o erro cometido na extração da raiz enésima de a, em que não existe uma potência de grau n, n inteiro, de b que seja igual a a (por exemplo: raiz quadrada de 2 cujos valores aproximados podem ser 1; 1,4; 1,41; 1,414; …);
- Raízes de índice par pode não ter solução válida no conjunto dos números reais (por exemplo: a raiz quadrada de -1, uma vez que a potência de grau par de um número é sempre positiva);
- Para dar consistência ao cálculo de raízes de índice par e radicando com valor negativo, foi criado o conjunto dos números complexos, com a introdução da unidade imaginária i, cujo valor corresponde à raiz quadrada de -1;
- Valor aritmético ou valor absoluto de um radical é o valor positivo desse radical (exemplo: o valor aritmético da raiz quadrada de 4 é +2, embora -2 também satisfaça a definição);
- No cálculo dos radicais, conjunto de operações com números irracionais e com expressões algébricas, são considerados sempre apenas o seu valor aritmético, ou seja, seu valor positivo. Os valores positivos e negativos, quando é o caso, são adotados principalmente na resolução de equações polinomiais, como por exemplo, em uma equação do segundo grau;
- Radicais equivalentes são os que têm o mesmo valor aritmético (exemplo: raiz cúbica de 8 e raiz quadrada de 4 são equivalentes por que ambas têm valor aritmético igual a 2);
- Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando. Veja exemplo abaixo.
Exemplos:
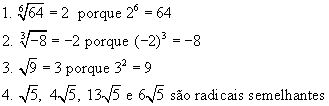
PROPRIEDADES
Apenas algumas das propriedades abaixo serão demonstradas, deixando a verificação das demais como exercício. Havendo manifestação de interesse poderei publicar um post específico com a verificação das propriedades não apresentadas.
P1. A raiz enésima do produto a.b é igual ao produto das raízes enésimas de a e b:
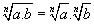
Demonstração:
Da definição de radiciação, temos que:
Por outro lado, utilizando-se a propriedade da potência de grau n de um produto, e, novamente, a definição de radiciação, obtemos:
Como se vê dos passos anteriores, foi demonstrado que ambos os lados da igualdade da propriedade elevado ao expoente n é igual ao produto a.b. Portanto, a base dessas potências são necessariamente iguais e a verificação da propriedade está concluída.
Aplicação prática da Propriedade (simplificação de radicais):
P2. O produto das raízes de a e de b com o mesmo índice n é igual a raiz enésima do produto a.b (note que esta propriedade é a recíproca de P1. Nas demais propriedades a recíproca também é válida. Esclarecimentos do que se entende por recíproca você pode obter no artigo sobre Potenciação ):
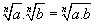
A demonstração de P2 é semelhante à de P1.
P3. O quociente de raízes de mesmo índice n é igual a raiz enésima do quociente dos radicandos:
P4. A potência de grau m da raiz de índice n de a é igual a raíz de índice n de a elevado à potência m:
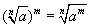
Demonstração:
Para demonstrar a propriedade P4 utilizarei a técnica de demonstração por indução sobre m, considerando n fixo, que consiste em:
1. A propriedade é verdadeira para m = 0, pois
2. Considerando que P4 é verdadeira para m = p, m > 0, isto é:
provemos que é verdadeira para m = p + 1, ou seja:
De fato:
Observe que na expressão acima utilizamos a hipótese (verdadeira para m = p), a propriedade P2 e a propriedade de produtos de potências de mesma base.
3. Considerando agora m < 0 façamos -m = q > 0, então:
Na expressão acima foram utilizadas a propriedade de potência de expoente negativo, a hipótese, a propriedade P3 e regra de divisão de frações.
P5. A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a:
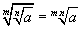
P6. A raiz enésima de a elevado a m é igual a raiz de índice p.n de a elevado a p.m obtida multiplicando-se o índice e radicando por p. A mesma propriedade é válida para a divisão:
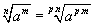
Exemplo: Redução de radicais ao mesmo índice
P7. A raiz de índice n da potência de grau m de a é igual à potência de grau m/n de a:
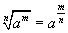
Demonstração:
Da propriedade P6, dividindo-se o índice e o radicando por n:
Exemplos:
É interessante observar que todas as propriedades de potências para expoentes inteiros positivos são válidas, também, para as potências de expoentes fracionários.
Referências:
- Abecedário da Álgebra (Volume 1 – Ciclo Ginasial), Darcy Leal de Menezes, Rio de Janeiro, Departamento de Imprensa Nacional, primeira edição, 1959;
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.
Artigos Relacionados:
- Questionarious #1 – Potenciação e Radiciação
- Curiosidade Matemática #5 – Método de Pitágoras para Calcular a Potência de Grau 2 de um Número
- Exercícios Resolvidos #3 – Radiciação
- Exercícios Resolvidos #1 – Potenciação
- Logaritmo
- VICHE Responde #1
- Potenciação
Posts relacionados trazidos a você pelo Yet Another Related Posts Plugin.
Categorias: AJAX,Matemática,Notícias Expressas,Pessoal,Técnico
Imprima este artigo
Envie este artigo para um(a) amigo(a)
194.289 views
185 Comentários Adicione o seu
1. Maujor&hellip | março 26th, 2006 at 09:52:09
Mais uma brilhante aula de matemática do mestre Newton!
Minha sugestão para o nome da seção a ser criada:
Viche responde
2. Watson Meyer&hellip | março 27th, 2006 at 12:21:56
Concordo!!!!
Mais uma brilhante aula, minha sugestão é : Aprendendo com viche
3. Joseny Freire de Carvalho&hellip | março 28th, 2006 at 15:42:08
Newton,
Gostei muito da explicação. Acredito que agora seja possível entender este assunto.
4. Naílson&hellip | março 28th, 2006 at 20:44:33
Esse é meu patrão!!!
5. ELIANA LOPES MORAES&hellip | abril 6th, 2006 at 14:37:28
MUITO BEM EXPLICADO.TENHO QUE FAZER UM TRABALHO E GOSTARIA DE TER EXEMPLOS MAIS FACEIS…OBRIGADO
6. Efigenia Aparecida Ciolin&hellip | abril 9th, 2006 at 18:27:35
Valeu! Conseguí resolver dúvida sobre Raíz enésima. um abraço.Efigênia. Belo Horizonte(MG).
7. Zeno Ferreira Borges&hellip | abril 10th, 2006 at 17:26:06
Gostei muito do conteúdo, a explicação é muito clara e torna fácil o assunto, estou estagiando para conclusão do último ano do curso de Licenciatura de Matemática e repassarei esse novo método de explicação sobre raiz enésimas aos meus alunos.
O nome que sugiro é Aprendendo Raizes Enésimas com Viche.
Zeno Ferreira Borges – Universidade Estadual de Goiás – Posse – GO.
8. Samira&hellip | abril 12th, 2006 at 11:40:56
adorei esse site de pesquisa.. aqui encontrei tudo que eu queria para poder fazer o meu trabalho de matemática.
obrigada.
voltarei sempre aqui…
beijos e abraços..
samira
9. Cleidmar&hellip | abril 12th, 2006 at 23:53:05
Consegui desevolver junto com o colega Zeno,demonstrações interessantes de raizes com espoesnte m
10. Cleidmar&hellip | abril 12th, 2006 at 23:56:06
Consegui desevolver junto com o colega Zeno,demonstrações interessantes de raizes com indices m
11. Viche » Equações &hellip | abril 16th, 2006 at 14:35:47
[...] INTRODUÇÃO Seguindo a ordem natural dos artigos sobre Potenciação e Radiciação será abordado agora as equações exponenciais. Antes, será fornecida uma breve noção sobre o conceito e propriedades da função exponencial. Considera-se, também, como pré requisito para o entendimento deste artigo o conceito de função. [...]
12. thiago&hellip | abril 22nd, 2006 at 18:58:23
ESTE SITE É SHOW DE BOLA ENCONTREI TUDO O QUE EU QUERIA ,AQUI FIZ O MEU TRABALHO PELO SEU SITE E FECHEI VALIAM 10,00 TIREI 10,OO.CONTINUEM ASSIM ABRAÇOS THIAGO.
13. Viche » VICHE Respo&hellip | abril 29th, 2006 at 01:02:28
[...] Como se trata de uma questão que traz embutida um certo grau de curiosidade e aparente complexidade, decidi iniciar com ela a abertura de uma nova categoria de posts. O nome escolhido para batizá-la, VICHE Responde, foi o sugerido pelo Maujor nos comentários do artigo sobre Radiciação. [...]
14. ALANA BELÃO&hellip | maio 5th, 2006 at 02:03:58
PRECISO FAZER UM TRABALHO DE MATEMATICA SOBRE RADICIAÇÃO COM NUMEROS NATURAIS,INTEIROS, RACIONAIS, IRRACIONAIS E REAIS.
15. BRUNA&hellip | maio 7th, 2006 at 20:59:38
QUERIA APRENDER POSSO DAR UM EXEMPLO AI VAISO QUE TEM QUE FAZER AI VAI A EXPRESSAO (8MAIS 5 RAIZ DE 2)VEZES (8 MENOS 5 RAIZ DE 2) MENOS (1 MAIS RAIZ DE 3) VEZES (1 MENOS RAIZ DE 3)
16. Belmiro Cavalcante Machad&hellip | maio 19th, 2006 at 18:24:47
Adorei.
Muito legal.
Valeu.
Estou estagiando no Ensino Médio para conclusão do Curso de Licenciatura Plena de Matematica, Regime Especial, da Universidade Estadual do Piaui – UESPI – Núcleo de Tabocas do Brejo Velho-Ba. Estamos concluindo nosso curso agora em julho/2006. Repassarei esse novo método de ensinar aos meus colegas.
Abraços.
Belmiro – Tabocas do Brejo Velho-Ba,
outro e-mail-msn = belmiromachado2@hotmail.com
17. Viche » Frações I&hellip | maio 21st, 2006 at 18:25:17
[...] Para que o entendimento seja mais efetivo é imprescindível o conhecimento das propriedades de Radiciação e Potenciação, dentre outros conceitos que serão apresentados mas não demonstrados, por fugirem ao escopo da matéria. [...]
18. makakita&hellip | maio 22nd, 2006 at 18:12:04
muito bom para o entendimento da populacao moderna que usa internet um grande meio de estudo via cabo! continuem assim pois cresceram no mercado de trabalho se tornado um grande site!
aee mano eh nois lado a lado nois ate o fim
=)
jeuhuhuehuehuehuehehuhe
19. MARTA&hellip | maio 26th, 2006 at 14:02:20
O que gostaria de saber seria algo sobre o radical
20. Deise Prospero&hellip | maio 27th, 2006 at 20:41:14
gostaria que demonstrasse que a propriedade 3 é irracional
21. Marinete&hellip | maio 27th, 2006 at 22:14:05
gostaria de saber se raiz quadrada de 2/3 é irracional e como posso demonstrar…
Ficaria grata se tirasse minha duvida
22. Newton de Góes Horta&hellip | maio 27th, 2006 at 23:11:56
Marinete,
Os números irracionais são números com infinitas casas decimais que não se repetem periodicamente, ou seja, os números que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:
raiz quadrada de 2 = 1,4142135…
raiz quadrada de 3 = 1,7320508…
Portanto a fração que tem como numerador a raiz quadrada de 2 e como denominador a raiz quadrada de 3 é uma fração irracional e, consequentemente, irracional. Você pode ver maiores detalhes no artigo Frações Irracionais e Racionalização.
23. Ph&hellip | maio 29th, 2006 at 19:51:32
manero
24. Carlos A C Ferreira&hellip | maio 29th, 2006 at 19:57:08
O resultado de 2 + raiz quadrada de 2 dividido por 2 – raiz quadrada de 2 é igual a 2 raiz quadrada de 2 ou igual a 3 raiz quadrada de 2??? Obrigado.
25. Priscila&hellip | maio 31st, 2006 at 12:29:08
Em *Definição – *Exemplos – *nº2, pelo menos no que pude observar, o resultado está errado.
(-2)^3 não é igual a 8 e sim a -8.
26. Newton de Góes Horta&hellip | maio 31st, 2006 at 13:55:08
Priscila,
Você está com toda a razão. Será corrigido o mais breve possível. Obrigado pelo aviso.
27. dete&hellip | junho 2nd, 2006 at 23:46:11
Gostaria que vcs me ajudasse em entender essa questão:
número irracional tem representação decimal infinita e não periódica e um número racional tem representação decimal finita ou infinita e periódica. O que aconteceria se não estivessemos num sistema decimal? E como representar 1/3 e 1/2 na base 2?
obrigada
28. Newton de Góes Horta&hellip | junho 3rd, 2006 at 14:29:45
Dete,
A resposta à sua questão implica em dissertar sobre sistemas de numeração. Portanto recomendo, para sanar sua dúvida de imediato, uma pesquisa no Google ou outro software de busca, onde você, certamente, obterá um farto material sobre o assunto.
A título de esclarecimento, se é que você não sabe, o sistema de numeração binário (ou de base 2), composto somente dos dígitos 0 e 1, é o sistema utilizado no mundo digital (computadores e outros), fortemente presente no nosso cotidiano.
Outros exemplos de sistemas de numeração são o octal (base 8 ) e o hexadecimal (base 16). Este último composto dos algarismos 0 a 9 e das letras A, B, C, D, E e F.
29. joelson do vales miranda&hellip | junho 21st, 2006 at 09:10:39
como vai eu não sei para quem estou enviando esta mensagem mias boa sorte
30. Raíssa&hellip | junho 21st, 2006 at 17:29:42
é parece que newto é um grande professor!!
31. William&hellip | julho 5th, 2006 at 15:42:47
Alguém sabe o processo como se tiva raiz pelo método de divisão? Ex.: raiz de 79
32. William&hellip | julho 5th, 2006 at 15:44:12
correção: tira
33. HENRIQUE&hellip | julho 27th, 2006 at 14:05:58
Caro amigo, senti falta da demonstração de RADICAL DUPLO. Um exemplo prático de como se transforma em radical simples. Se puder me manda … Obg.
34. Newton de Góes Horta&hellip | julho 29th, 2006 at 17:28:11
[...] Resolução de exercícios sobre Radiciação com o objetivo de fixar os conceitos e as propriedades já tratadas no artigo de mesmo nome. Inicia com a questão do leitor identificado como HENRIQUE (comentário #33) sobre raiz de índice m da raiz de índice n ou como dito por ele, radical duplo. [...]
35. karla de oliveira marinho&hellip | agosto 15th, 2006 at 16:52:53
Gostaria de saber sobre a historia dos radicais-origem………
obrigada!!!!!!!
36. Tarcy&hellip | agosto 17th, 2006 at 08:54:57
Como posso resolver esa equação irracional 2V-x=12
37. Amanda Maciel&hellip | agosto 19th, 2006 at 07:59:44
Gostei muito das explicações, espero que esteja sempre atualizado,pois me ajudou muito…
38. Sara&hellip | agosto 20th, 2006 at 15:23:18
Realmente uma excelente explicação. Clara e objetiva !
39. thais irene felipe maia&hellip | agosto 27th, 2006 at 12:10:57
queria saber porque não estão mostrando neste saite radiciação com numeros racionais(fração)
40. Daniel&hellip | setembro 2nd, 2006 at 12:30:06
Gostaria e saber a respeito dessa equacao, raiz cubica de cinco no denominador e raiz cubica de nove no numerador.
Como resolvo este problema com indice n>2.
41. Patty&hellip | outubro 7th, 2006 at 12:02:59
Como se lê a fração de 1 sobre 200 ????
42. carolina da costa&hellip | outubro 14th, 2006 at 21:18:42
Perfeito,acho que estou aprovada vou tirar A.achei tudo o que necessitava.
43. gilmar alves da cunha&hellip | outubro 24th, 2006 at 15:10:40
gostei muito das suas explicaçoes, mas gostaria que mandasse mais exercicios.
44. izaulino&hellip | dezembro 8th, 2006 at 23:20:41
gostei muito das exesplicaçoes sao muito claras espero que continue sempre assin. achein tudo o que eu precizava. esse trabalho vale 30 pts, tenho certeza de que vou conseguir esses 30 pts. muito bom valeu
45. THIAGO&hellip | dezembro 15th, 2006 at 13:22:54
Olá professor sei que você consegue resolver este problema,
porque eu preciso ter certeza da resposta
“5 sobre raiz cúbica de sete ao quadrado” se poder responder ficarei muito grato. obrigado
46. carlos&hellip | fevereiro 9th, 2007 at 11:08:36
kra muito bom esse site explicou e me ajudou muito
=)
vlw pelas explicações
47. alberto&hellip | fevereiro 24th, 2007 at 06:21:00
Gostaria de saber como resolver a seguinte questão.
Raiz quadrada de 2 + raiz quadrada de 2 + raiz quadrada de 2 +…
Se possível explicar passo a passo.
48. lyvia&hellip | fevereiro 25th, 2007 at 13:22:54
professor!!eu tenho dúvida quando o expoente eh decimal….eu sei que pode transformar em fração…mas complica um pouco! vc poderia me dar umas dicas???muito grtaa
49. jamille&hellip | fevereiro 25th, 2007 at 15:49:54
como posso resolver a expressão 15 expoente negativo 1 menos um meio
50. Brenon Alexandre&hellip | março 5th, 2007 at 21:11:45
Qual é a raiz de 2….
Como faço pra achar a raiz de números assim?…Raizes irracionais…
51. edna&hellip | março 14th, 2007 at 23:01:48
gostaria que me ensinasse resolver a seguinte equação:
raiz cúbica de: dois elevado a 28 somado dois elevado 30 e tudo dividido por dez
52. Raphael&hellip | março 16th, 2007 at 20:54:23
gostaria que me ensinasse resolver a seguinte equação:
raiz cúbica de: dois elevado a 28 somado dois elevado 30 e tudo dividido por dez
53. Célio Antonio da silva&hellip | março 16th, 2007 at 22:15:31
Gostei muito do sait , mais tenlho que fazer um trabalho para escola e noa estou coseguindo resolver gostaria de saber se vc me ajuda nesse exercicio Raiz enesima
Semplifique a expressaõ
__a.b.(a.b).(a.b)_____
(ab) (a.b)
54. Raphael&hellip | março 17th, 2007 at 15:32:56
Muito obrigado pela resposta, o site é d+.
55. Cami&hellip | março 18th, 2007 at 15:52:05
O Site eh muito legal e produtivo..
mas eu gostaria de saber a raiz enesima de EU!!
Se souberem e puderem me mandem a resposta!!
obrigada!!
=)
56. hiago&hellip | março 18th, 2007 at 21:15:36
ruim explicaçao,nao entendi quase nada…..
57. Marcio&hellip | março 20th, 2007 at 23:59:18
Ola amigo…
Gostei muito do seu site, so que gostaria de uma ajuda sua:
Tenho que provar que a raiz enezima de n esta entre 1 e 2 e gostaria de uma ajuda ou para fazer ou de uma fonte que possa me ajudar
A questão seria provar que 1 ≤ ⁿ√n ≥ 2
Obrigado
58. deyse&hellip | março 26th, 2007 at 10:46:11
adorei essa matéria continuem assim bjos
59. Ana Cláudia&hellip | março 28th, 2007 at 14:29:42
Acho essa esplicação muito boa mesmo.
60. hiago&hellip | abril 1st, 2007 at 23:27:27
como é chamado o nome dos termos da raiz quadrada
61. Nathália&hellip | abril 9th, 2007 at 19:05:00
Bá…
Estava com mtu duvidá em matemática tirei tudu…
Muito Obrigado!!!
62. Jessica da Silva Porfirio&hellip | abril 10th, 2007 at 11:04:06
esse site é bom
63. patricia&hellip | abril 10th, 2007 at 11:09:59
quem trabalha com radiciação?
64. amanda&hellip | abril 10th, 2007 at 16:37:52
como que é usado radiciação em nosso dia-a-dia??
65. Lígia&hellip | abril 11th, 2007 at 19:14:40
Por favor estou tentando resolver este problema, mas não sei como
raiz cúbica de: (2 elevado a 28 + 2 elevado a 30) /10
66. Lígia&hellip | abril 12th, 2007 at 10:06:59
Muuuuuuuuito obrigada!!!!!!!!!!!!!!!!!!!!!!!!!!
67. Naiara&hellip | abril 12th, 2007 at 14:48:32
Olá!
Gostaria muit de aprender como extrair a raiz qudrada de numeros decimais.
15,80 por exemplo, acho super confuso o processo e em provas de concurso não utilizamos calculadoras.Se puder me ajudar mostre-me passo a passo!
Abraços !
68. Milena&hellip | abril 14th, 2007 at 07:52:28
Olá…
Muito legal esse site…
Me ajudou muito! Naum estava axando sobre radiação em lugar nenhum mais aki eu Axei…
Parabéns para o(os) Dono(os)
BjuH!
Obrigada!
:)
^~^
69. Patricia Belchior&hellip | abril 24th, 2007 at 10:14:26
aaaaaaaaaaaaaaaxei tudo o que queria e com certeza vou me dar muito bem na prova, e um site descomplicado, com boms bizus…. quero mais dicas , ponham mais,…quanto mais melhor…
agora é 10!
70. DONIZETE&hellip | maio 1st, 2007 at 17:12:11
FAVOR , QUERIA SABER COMO RESOLVO ESSA EQUAÇÃO
2,5 VEZES A RAIZ DE X MENOS A RAIZ DE X IGUAL A 1,5, QUAL É O VALO DE X
(2,5*VX-VX=105, QUERO ACHAR O VALOR DE X )
71. luara&hellip | maio 1st, 2007 at 20:06:22
bah, até pra mim, uma estudante de oitava série, ajudou bastante as explicações!!!
valeu!
72. Gabriel Cardoso De Aguia&hellip | maio 8th, 2007 at 21:35:58
vlw esse site me ajudou muito apesas de eu nao gostar de matematica…
73. thayna loisi&hellip | maio 16th, 2007 at 21:58:53
como fazer esta conta? 2
-sinal de raiz quadrada 1-(-3)
5
74. Airton&hellip | maio 26th, 2007 at 19:22:20
Muito bom e prático é realmente muito competente. Professor ajude-me a realizar o cálculo de potência com base em inteiro e expoente em decimal tipo: 2^1,25. Agradeço desde seu retorno.
75. marcos&hellip | maio 29th, 2007 at 19:17:51
so apaixonado pro numero parabe´ns para os construtores edste site show wwwwwwwwwww wwwwwwwwww wwwwwwwww wwwwwwwww
76. LIDER PANDA&hellip | junho 21st, 2007 at 16:37:26
Gostei imenso do vosso trabalho, e bastante proveitoso para mim. mas achei nao estar certo, ali a raiz cubica de -2 ser =a 8
prque um numero negativo com expoente impar sera sempre negatvo o resultado.
77. Paulo&hellip | junho 24th, 2007 at 07:24:21
mas que porcaria de trabalho vcs devia estudar um pouco mais antes de lançar essas porcarias na internet
78. rodrigo&hellip | junho 24th, 2007 at 18:48:08
naum gostei muito
79. Amazing Autos Guide&hellip | agosto 24th, 2007 at 05:00:25
Amazing Autos Guide
I couldn’t understand some parts of this article, but it sounds interesting
80. Edson&hellip | agosto 28th, 2007 at 21:59:41
Como fazer para eliminar um radical de indice negativo?
Ex- log de 8000 na base x = -6. isso cai em um radical de indice negativo, mas a resposta é raiz quadrada de 5 sobre 10.
Estou encontrando raiz de 5 com indice negativo -2 sobre 2. Qualquer um dos dois que se elevar a -6 chegará ao 8000.
81. ronei de freitas gonçalv&hellip | setembro 2nd, 2007 at 07:35:14
bom eu achei bastante interesante essa materia cheia de interatividade .
82. magdiel&hellip | setembro 2nd, 2007 at 15:51:35
por exemplo raiz cúbica de 3 elevado a 15 mais raiz cúbica de 3 elevado a 14 mais raiz cúbica de 3 elevado a 13 dividido por 39.
se alguem souber simplificar postar o calculo vai
obrigado
83. Isaque José&hellip | setembro 27th, 2007 at 01:47:34
Eu achei esse site horrivel pq ñ dá para vc tirar suas duvidas!!!
84. Margarida Luz&hellip | setembro 27th, 2007 at 19:01:15
Estou digitando um trabalho de matemática e não consigo encontrar o radical em inserir símbolos. O programa do meu computador é o microsoft Office Word 2007. Nem encontrar aquele lapisinho para desenhar eu consigo.
Gostaria que me enviasse por e-mail ou me orientasse como fazer ou encontrar.
Antecipo agradecimentos.
85. allan&hellip | outubro 8th, 2007 at 14:15:29
Viche, por favor, me de a resposta dessa equação:
(8+5.raiz 2).(8-5.raiz 2) – (1+ raiz 3).(1- raiz 3) = ??
seria 10 a resposta?
Obrigado
86. Ana Lucia&hellip | outubro 15th, 2007 at 14:50:11
ACHEI LEGAL
87. jean carlos&hellip | novembro 6th, 2007 at 17:02:58
como resolvo fraçoes de divisao
88. Brenda&hellip | novembro 10th, 2007 at 16:30:46
O que é raiz cúbica??
89. henrique&hellip | dezembro 3rd, 2007 at 17:58:28
adorei o site, fizuma boa prova revisando aqui
90. Adalberto&hellip | dezembro 9th, 2007 at 18:41:45
Gostaria de saber: 2 vezes raiz de 3?
91. pablo&hellip | dezembro 20th, 2007 at 14:02:06
eu achei muito legal
92. RAFAEL&hellip | janeiro 18th, 2008 at 06:46:38
VALEU ME DEU UMA GRANDE AJUDA
93. Jéh&hellip | fevereiro 21st, 2008 at 12:47:01
Eu gostei bastante do site…
mas só um toque pros donos….
O site é mto bom, mas parece estar abandonado..
Mta gente com dúvida e ning pra responder..
Minha dúvida é a msma q muitos aqui…
Mas pra que vou perguntar se ja fizeram a msma pergunta a 6 mesese ninguem respondeu!
Mas msm assim gostei mto!
94. Luzia do Carmo Rosa&hellip | fevereiro 26th, 2008 at 19:40:09
Muito bom. Gostei porque encontrei o que estava procurando.
95. Silvanesa&hellip | março 7th, 2008 at 17:16:49
gostei das explicações e dos esquemas,quero que mandem p/ a meu email esquemas como esse p/ q eu possa estudar .
bejãoooooooooooo
96. olga lima borges moura&hellip | março 9th, 2008 at 02:23:25
gostaria q voces me descem a opcao de um jogo matematica q nele tenha incluindo radiciaçao……
mas mesmo assim adorei o seu conteudo…
valeu
97. Érica Bohn&hellip | março 9th, 2008 at 19:25:12
Tenho um exercício no livro de mat. q não consigfo resolver….
já “rabisquei” umas 5 folhas e não consigo achar um meio pra chegar ao resultado q SEI q é 2 elevado à 9….
Se for possível gostaria de saber como chegar à esse resultado, pq o q não acho é o meio…
Desde já agradeço!
98. Érica Bohn&hellip | março 9th, 2008 at 19:26:24
Tenho um exercício no livro de mat. q não consigfo resolver….
raiz cúbica de (2 elevado à 28 + 2 elevado à 30) / 10
já “rabisquei” umas 5 folhas e não consigo achar um meio pra chegar ao resultado q SEI q é 2 elevado à 9….
Se for possível gostaria de saber como chegar à esse resultado, pq o q não acho é o meio…
Desde já agradeço!
99. Mariana&hellip | março 11th, 2008 at 21:16:22
Estudei matematica por sua explicação
Posso tira uma boa nota, aleu, vc consegue explica isso até pra quem naum sabe nada (EU)
100. ricardo&hellip | março 14th, 2008 at 18:17:56
valeuuuuuuuuuuuuuuuuuuuuuuuuuuu!!!!!!!!!!!!!!!!!!
101. camila&hellip | março 15th, 2008 at 18:16:39
odeiooooooooooooooooooooooooooooooo matematica
102. wellington&hellip | março 16th, 2008 at 18:00:27
o segundo exemplo esta erra (-2) elevado ao cubo. da -8 e nao 8
103. Elionara&hellip | março 23rd, 2008 at 19:51:24
oi professor. obg essa explicação me ajudou muito, salvou minha pele. bjão.
104. Felipe&hellip | março 31st, 2008 at 21:14:04
Oi,,sou um estudante da 8ª série q,incrivelmente,adora matemática.Gostaria de agradecer por esse site,que tirou uma dúvida mto grande de dentro de mim sobre Radiciação,MTO OBRIGADO!!!!
105. Ellen&hellip | abril 2nd, 2008 at 16:11:38
Eu nao consigo entender o que é radiciaçao
106. barbara&hellip | abril 3rd, 2008 at 12:05:29
como eu resolvo essa aii ó> raiz sexta ,o radical (a) com o expoente (7) x (z) com o expoente (13) ?
107. wevillen&hellip | abril 3rd, 2008 at 13:21:09
qual e a raiz quadrada de 32?
108. eder&hellip | abril 3rd, 2008 at 22:43:07
eu não achei oque eu estava procurando
109. Izabela&hellip | abril 7th, 2008 at 15:51:25
está muito bom!
mas se explicasse com mais clareza iria ser mais fácil de entender!!
110. kredinilson&hellip | abril 9th, 2008 at 12:12:30
achei muito podre esse site!!!!!!!!!!
q site de 5 categoria………shahsahshasahshsah..
111. edemária&hellip | abril 9th, 2008 at 21:00:41
obrigada quem quer que seja.
112. Rana Gavino&hellip | abril 16th, 2008 at 21:04:27
Muito bom …
Me ajudou bastante a relembrar alguns fatores sobre radiciação q tinha esquecido …
MUitoo bom ..
Abraços e beijos ..
113. roger rosa&hellip | abril 24th, 2008 at 19:26:41
ahhh foi bom ter pesquisado ai pqeu inha que fazer um adependencias e nao tava a chando nada e soh entcontrei aqui vcs precisa ter tbm sobre radicalização de denominadores sobre matématica
114. jullyana büttenbender&hellip | maio 2nd, 2008 at 17:09:56
vc poderia me repassar um exemplo de simplificaçôes ds radicais
por favor me repasse URGENTE
eu estou precisando
115. Noel Barreto&hellip | maio 3rd, 2008 at 16:12:01
Amigos,
Tenho a seguinte questão a resolver: a=raiz décima segunda (12) de 1,84. São dadas as seguintes informações:
a) Raiz cúbica de 1,84=1,22538514.
b) Raiz quarta de 1,84=1,1646742.
c) Raiz sexta de 1,84= 1,10697115.
Com base nestas informações qual propriedade da radiciação eu poderia utilizar para a resolução da questão?
Agradeço se puderem me ajudar.
Noel Barreto.
116. xico&hellip | maio 8th, 2008 at 14:35:42
muito bom
117. augusto&hellip | maio 8th, 2008 at 16:59:35
qual o resultado de:
raiz cúbica de a/b e dentro dela raiz quadrada de a/b?
118. ruan&hellip | maio 15th, 2008 at 11:59:03
peeelo amor de deus.. me ajudou demais essa explicação.. primeira vez que visito esse site.. ta de parabens cara! =D
abraços pra todos.
119. Ana Luiza&hellip | junho 23rd, 2008 at 20:42:52
Nossa adorei o site,eu estava com duvida,acabei lendo e entendendo!!!obrigada
120. EDIMILSON SANTOS SILVA&hellip | julho 5th, 2008 at 07:00:40
DIRETO, COERENTE E SIMPLES.
Muito bom material, você me fez lembrar de um antigo professor de matemática, foi este professor que me abriu o entendimento e me fez gostar de matemática.
Já pensou em escrever um livro didático para matemática, talvez você já o tenha feito e eu é que não o conheça! Deixei o banco das escolas há mais de 50 anos.
uma das principais causas do péssmo grau de aproveitamento no ensino brasileiro na área de matemática é que a maioria dos livros didáticos de matemática são escritos para quem já conhece matemática, daí vem o desastre! Os autores de livros de matemática fundamental utilizam a linguagem matemática para explicar matemática, como fazem isto logo no princípio do aprendizado de matemática a maioria dos alunos tomam ojeriza pela área e adeus bons alunos de matemática, se você se propor a publicar o livro para o ensino de matemática! Pode utilizar o pomposo título: DANDO NOME AOS BOIS, (matemática simplificada), vai ser um sucesso…
A propósito, a palavra é devagarzinho.
Edimilson
121. João Valentim Barbo&hellip | julho 5th, 2008 at 22:43:09
Eu acho muito interessante professor nenhum ensinar nas escolas, como se calcular a raíz quadrada sem o uso de
calculadoras. A raíz cúbica então, nem se fala.
Por experiência própria, me lembro perfeitamente, quando
fazendo o curso de MADUREZA na década de 70, pedí ao
professor p/ explicar como calcular a raíz quadrada de um
número. O mesmo “enrolou” até o fim do ano sempre com uma
desculpa, mas nunca explicou nada.
Aprendí com muito custo, depois de vários anos numa
matéria que encontrei na INTERNET e ensinei meu filho,
KLEBER AUGUSTO BARBO a extrair essa raíz, já explicando
que na escola ele jamais iria aprender.
Hoje, ele é mestre na arte da extração da raíz quadrada a
ponto de desconsertar sua professora. Quero apenas dizer
que meu filho tem apenas 11 anos e grande capacidade de
aprendizado.
Por que ninguém fala nada sôbre a raíz cúbica, sem usar
a fórmula de NEWTON, que é desesperadora?
Quero acreditar que a raíz cúbica deva ser parecida com
a raíz quadrada, na fórmula, ou será tão diferente assim?
João Valentim Barbo
122. Karinne de Oliveira Carva&hellip | agosto 5th, 2008 at 14:18:53
gostaria que voces falassem sobre as propriedades dos numeros reais e radicais pois eu tenho trabalhos de matematica que pede este conteudo e nao tem obrigada pela atencao
atenciosamente :
Karinne de Oliveira Carvalho
123. sebastiao de jesus neto&hellip | setembro 1st, 2008 at 15:55:00
voces estao de parabens pelas publicaçoes escelentes sobre as materias de matematica que têm fornecido à gente. gostaria que passacem a passar exercicios ao meu e-mail.
124. juliio Faria&hellip | setembro 2nd, 2008 at 12:35:07
O trabalho é muito bom. No entanto seria perfeito se houvesse uma seção onde enviássemos dúvidas e elas fossem respondidas para todos. Assim ampliaria exponenciamente o conhecimento dos internautas.
Obrigado
julio
125. rogth&hellip | setembro 6th, 2008 at 13:25:40
oi, Tudo bem?gostei do seu artigo ele explica detelhadamente o básico sobre raiz, mas eu gostaria de saber o seguinte:
como é q prova q a raiz enesima da raiz enesima …… de um numero “a” é igual a 1
126. Cleide Mara&hellip | setembro 28th, 2008 at 14:42:17
Por favor gostaria de saber como posso resolver a seguinte questão: Raiz cúbica de 2 elevado a 28 mais 2 elevado a 30 dividido por 10. Se puder me ajudar agradeço muito. Obrigada.
127. Adriana Silva&hellip | outubro 7th, 2008 at 15:12:31
Gostaria de ter uma ajuda para fazer esse programinha.
Faça um programa que leia um número inteiro X e
um expoente inteiro n.
O programa deve calcular e exibir o resultado,
ou seja X elevado a n.
obs: usar uma estrutura de repetição
Plz! Ty!
128. roger&hellip | outubro 14th, 2008 at 12:27:08
por favor, vc poderia passar pra mim exemplos de simplificaçôes ds radicais, tenho muitas dúvidas a repeito.
Obrigado!
129. karina fernandes teixeira&hellip | outubro 16th, 2008 at 16:51:44
oi,eu entendi muito bem,mas eu estou proucurando uma forma de resolver a seguinte questão: raiz cubica de três elevado a um vírgula cinco.
já tentei de tud e nao consigo resolver.
gostaria q vc me ajudase.
obrigado.
130. teko&hellip | dezembro 10th, 2008 at 15:12:26
a ajuda foi boa vlw
131. Felipe D&hellip | janeiro 13th, 2009 at 22:23:34
Estou com a seguinte dúvida: raíz quarta de 2 multiplicada pela raíz quadrada de seis é igual a dois elevado a três quartos multiplicado por três elevado a um meio?
Acho que esta igualdade não esta correta.
Quem puder me ajudar agradeço!
132. carloshenrique&hellip | fevereiro 4th, 2009 at 16:29:26
foi muito interessante passar por aq e saber muito mais
133. Juliana&hellip | março 4th, 2009 at 10:14:15
Ola..eu tenho alguns problemas com fatoraçoes algebricas. Quem puder me ajudar..eu agradeço!! =D
134. artemiza&hellip | março 15th, 2009 at 15:29:24
gostei da materia e muito lagal p apredremos mais sobre fatoracoes e a raizes etc………
135. Jéssica Bender Esteri&hellip | março 23rd, 2009 at 01:51:43
O que é uma raiz enésima?
136. simone&hellip | março 24th, 2009 at 17:03:55
gostaria de ver exercicios de simplificações de radicais porque estou com difilculdades para entnder
137. tayna&hellip | abril 3rd, 2009 at 10:00:55
como calcula a raiz de 1/2????
138. mayarah&hellip | abril 5th, 2009 at 17:09:58
eu odeio matematica
139. jaqueline&hellip | abril 5th, 2009 at 20:06:36
Gostaria de mais conhecimento sobre simplificação de radicais ,
retirando fatores do radicando ! Desde já agradeço . ! ;)
140. Elaine Prudencio&hellip | abril 11th, 2009 at 16:52:09
ola pessoal, estou com dificuldade em chegar no resultado do seguinte exercicio.
raiz quadrada de nove menos entre parenteses raiz de cinco elevado a sexta com expoente a um terço mais entre parenteses raiz quadrada de sete elevado ao expoente meio.
e ai como chego no resultado.
desde ja agradeço pela ajuda.
141. Mattias&hellip | abril 12th, 2009 at 15:52:05
Não consegui entender como calcular a raiz enesima de um numero qualquer. Os exemplos me parecem direcionados a facilitar a explicação, no entanto não fica claro como aplica-los. Por exemplo, como devemos proceder para calcular a raiz quinta de 342, cujo equivalente em potenciação será 342^1/5?
142. fernanda 2° ano "EM"&hellip | abril 20th, 2009 at 23:00:53
eu acho esse assunto muito interesante…
143. marina&hellip | abril 23rd, 2009 at 16:22:23
gostaria de saber como resolver RAIZ QUADRADA DE ( X elevado a 2 ) – 6x + 9
144. camila barros felix&hellip | abril 27th, 2009 at 11:13:45
a Paula a Yarlla e eu Camila barros amomos esse site…..
bjusssssssss3333333
888888 77777
+++++++
145. Salomao Alberto Mendes&hellip | maio 8th, 2009 at 17:14:01
Gostaria de agradecer por esta site de informacoes , principalmente na cadeira de matematica . contudo sugeria que adicionacem mas exercicios e debates.
Atentamente
Salomao Mendes
146. silvana&hellip | maio 9th, 2009 at 14:26:55
eu amo matematica!!mas ñ consiguo entender
147. willians campos&hellip | maio 24th, 2009 at 14:06:44
estou cursando matematica,e gostaria de uma orintação de como fazer para escrever as regras e as definições de potenciação para que os alunos de sexta serie possam ler e entender de forma mais simples e mais rapidas
148. Luisa&hellip | junho 2nd, 2009 at 20:34:35
Olha eu tenho uma duvida, como isso pode se aplicar no nosso cotidiano, ja procurei em um monte de site e nao achei nada. Me ajua?
149. Tiago&hellip | junho 4th, 2009 at 14:01:19
Pow,eu tenho prova hoje de matematica,como ta encima da hora ,eu estudei no caderno,e vim aki na net pra confirmar se eu aprendi mesm.obrigado pq eu ja aprendi vlw
150. Felipe Baltor&hellip | junho 10th, 2009 at 23:03:35
Olá, tudo bem? gostei bastante do artigo, tudo está muito bem explicado, mas minha dúvida não está nele, por isso acho que poderia perguntar. Eu estava estudando equaçõs do segundo grau e polinômios e estou com umas dificuldades de chegar a certos resultados… minha dúvida é sobre a diferença conceitual entre a²=x e a=raiz de x, com relação aos sinais.
Abraços
151. misa-misa&hellip | junho 20th, 2009 at 21:55:58
hmmmmmmmmm……………………..to perdidaaa
152. kyssia&hellip | junho 30th, 2009 at 20:58:19
massaa!!**
153. lucas&hellip | julho 5th, 2009 at 19:46:00
po tem prova de matematica amanham
valeu deu p tira muitos duvidas
154. Jhonny Jose dos Santos Le&hellip | agosto 30th, 2009 at 11:04:36
muito bom sua fomula de explicação!
155. Janaina&hellip | setembro 14th, 2009 at 15:22:27
Too perdidoona taambeiim (!)
156. Loka&hellip | setembro 30th, 2009 at 16:54:27
Legal mais msmo assim ñ sei fazer issso…
…Huashuasuahsuahsa…mias um dia eu aprendo..
…Vlw
157. Aline Branco&hellip | novembro 29th, 2009 at 12:06:10
to totalmente perdida :@
158. tiaginho10&hellip | novembro 30th, 2009 at 21:13:18
deu pra intender…….valeu
gostei
-tirou algumas dúvidas dos assuntos da recuperação de matematica-
159. RRR&hellip | fevereiro 20th, 2010 at 18:21:20
vc acha esse site legal?
160. Lissa&hellip | fevereiro 22nd, 2010 at 20:41:55
Gostei.. deu pra fazer o relatório rs
Valeu (:
161. calculo&hellip | fevereiro 27th, 2010 at 09:31:01
gostei so que queria tirar mais uma duvida, como calcular raiz quadrada de 2 x raiz quadrada de 2x raiz quadrada de 2
162. luciana santos souza&hellip | março 1st, 2010 at 15:07:11
na minha opinião esse site é importante para os e estudantes…..
tem assuntos na sala de aula que são difíceis
bjjjjjjssss!!!!!!!!
lululuzita
………………………………………………./;./;..~;.;./;./;.;.?:
163. Laaayrinha&hellip | março 3rd, 2010 at 14:26:54
Gostei doo siite :)) bem esclareido !
164. loko&hellip | março 4th, 2010 at 16:07:56
uhu facim e nao so nerd tiro nota baixa flw galera(isso nao me ajudou em nada¬¬)
165. Adriana de souza alves&hellip | março 11th, 2010 at 12:33:47
eu adoroooo fazer enesima!!!
166. Leon&hellip | março 15th, 2010 at 12:26:34
Não entendi nada, acho qe esse negócio ai não é tão esclarecedor, já tem 30 minutos qe eu estou tentando entender alguma coisa disso e NADA. =D
167. izadora fernanda da silva&hellip | março 17th, 2010 at 16:44:45
na minha opinião esse site eé importante sim maiix ñ contém tudo o que um estudante precisa para aprender “RADICAIS EQUIVALENTES”! que era o que eu vim procurar!
168. Cassio&hellip | março 18th, 2010 at 01:36:46
Ok. Mas na expressão “a” elevado a potência “n” =b, como calacular o valor de n?
ex.: 2n=32 (2 elevado a n é igual a 32). qual o vaor de n? como calcular?
169. Clara Mara&hellip | março 20th, 2010 at 17:46:44
Mas quem fez essa teoria, tão incrível?
170. mariely&hellip | março 25th, 2010 at 15:04:49
a radiciação é o inverso da potenciação..
vcs diviam aprender isso na escola
vem fazer o trabalho com a gente pra ve como vcs vão aprender alguma coisa que o professor Paquito ensina.E a gente aprende viiu
ele eh um otimo professor pois a gente aprende muito com ele so naum sabe como fazer os exercícios e a introdução q a gente veio buscar aqui mais naum encontramos nada de bom
por favor alguem da proxima vez coloca algo q preste e q a gente consiga entender tah
obrigada xau
171. rafaele&hellip | abril 6th, 2010 at 12:47:45
muito bacana essas esplicacoes…..xau
172. Joana&hellip | abril 6th, 2010 at 20:28:00
não ajudo em nada¬¬
173. Pedro Simão&hellip | abril 16th, 2010 at 11:57:02
legal me ajudou muito.Mas será que vocês poderiam me enviar algumas questões que envolvam esse assunto ? De já agradeço.
174. Gabriella&hellip | abril 29th, 2010 at 15:04:55
bom , eu não enteendii muiitoo beem naa escoolaa , maais depois quee eu li essa explicação melhorou muiito ‘
Valeeeeu (y)
175. sidneiga&hellip | maio 1st, 2010 at 14:54:39
achei esta explicação a melhor de todas que encontrei na net, parabens.
176. Kelly&hellip | maio 5th, 2010 at 16:59:45
Oiie Gente (y)
Olha pessoal acho que ficou faltando assunto
Tipo, Quem inventou / Quando Surgiu etc..
177. Neusa&hellip | maio 6th, 2010 at 00:35:53
Muito boa matéria. Quem inventou não interessa. Mas que eu tô ficando boa nisso aí… Ah isso só as provas vão me dizer…
Obrigada para vc que criou este site!
Merece um beijãaaaaaaaaaaaaaaaaaaaaaaaaaaao…
178. Ulianov da Sillva&hellip | maio 12th, 2010 at 14:24:31
nunca pensei que encotraria matéria explicada de uma forma tão simples, tão simples e, mesmo a distáncia deu pra perceber tudinho valeu brother.
Ulianov da Silva- Luanda Angola
179. mayra&hellip | maio 18th, 2010 at 16:50:55
ñ~gostei nao ta explicando nada e nem tem exemplo
180. martta&hellip | maio 31st, 2010 at 10:28:24
estou na mira da cascavel
181. Julia&hellip | junho 10th, 2010 at 19:30:11
o site é bom, mas precisa de algo melhor explicado,
algumas coisas estao confusas….
Vlw
:)
182. Jamil&hellip | junho 16th, 2010 at 05:38:36
√4 = (+2)
√4 = (- 2)
Então: (+2) = ( -2) …????
183. moane&hellip | junho 17th, 2010 at 14:59:39
bom deu p entender,só espero num tirar + notas baixas esse site me ajudou muito a fazer a pesquisa.=D
184. Raquel&hellip | junho 29th, 2010 at 14:49:38
Bom, tá muito ótima a explicação, más eu quero saber certinho o QUE É RAIZ CÚBICA, e naum como se resolve!
Valew!
Bjinhos
185. DEICY NOGUEIRA&hellip | agosto 6th, 2010 at 17:06:42
LOEGAL………
DEU P/ TIRAR ALGUMAS DUVIDAS QUE EU TINHA…
Deixe seu Comentário
São permitidas as seguintes tags:
<a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <strike> <strong>
Trackback this post | Subscribe to the comments via RSS Feed