O Viche tem recebido visitas a partir de pesquisas efetuadas no Google com o termo triângulo em função dos artigos publicados sobre Tecelagem Popular no Triângulo Mineiro. Assim, com o objetivo de atender esse indicativo presente nas estatísticas do blog passo a escrever sobre conceitos relacionados ao termo mencionado: mais especificamente sobre Semelhança entre Triângulos.

Antes, vamos definir o que é congruência entre triângulos.

Congruência entre Triângulos

Dois triângulos (ou de forma geral, duas figuras planas) são congruentes quando têm a mesma forma e as mesmas dimensões, ou seja, o mesmo tamanho.

Já a semelhança entre triângulos, objeto do artigo, aborda o conceito mais amplo onde se tem triângulos com a mesma forma, mas não necessariamente com o mesmo tamanho. Em outras palavras, congruência é um caso particular de semelhança entre triângulos no sentido de que se dois triângulos são congruentes necessariamente eles são semelhantes, mas o contrário não é verdadeiro, como você observará daqui em diante.

Definição de Semelhança entre Triângulos

Dizemos que dois triângulos são semelhantes se, e somente se, possuem seus três ângulos ordenadamente congruentes e os lados homólogos (homo = mesmo, logos = lugar) proporcionais.

Triângulos Semelhantes

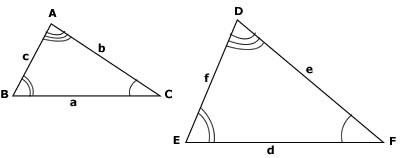
Traduzindo a definição em símbolos:

Definição de Semelhança entre Triângulos

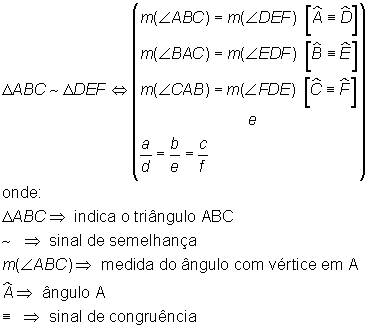
Observe que as três primeiras expressões entre os parêntesis indicam a congruência ordenada dos ângulos e a última a proporcionalidade dos lados homólogos.

Em bom português, podemos, ainda, definir a semelhança entre triângulos através da frase: dois triângulos são semelhantes se um pode ser obtido pela expansão uniforme do outro (caso deseje comprovar veja o programa em Java descrito abaixo).

Razão de Semelhança

Denominamos o número real k, que satisfaz as igualdades abaixo entre os lados homólogos, como a razão de semelhança dos triângulos:

Razão de Semelhança

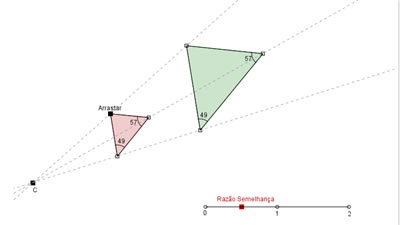
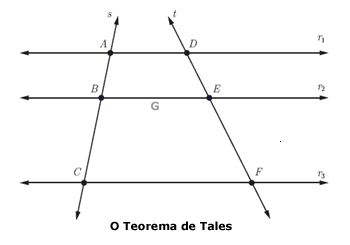
Para uma idéia melhor dos conceitos acima sugiro uma visita ao programa em Java de Karlos Gomes. A imagem inicial da página é apresentada a seguir, onde temos dois triângulos entre um feixe de três retas com origem no ponto C. Ao arrastar o triângulo rosa para cima ou para baixo, o ponto em vermelho no segmento de reta indica o valor da razão de semelhança correspondente. Ao colocar o triângulo rosa exatamente sobre o verde você observará que a razão de semelhança é igual a 1, como era de se esperar (você sabe dizer o significado deste fato?).

O único problema é que o programa demora a carregar. Tenha um pouco de paciência, e espere, vale a pena. Após, por favor, retorne a este artigo :-).

Semelhança de Triângulos

Exemplo

Dados os triângulos ABC e DEF semelhantes com as medidas dos lados indicadas abaixo, calcule as medidas dos lados e e d do segundo triângulo.

Exemplo de Semelhança

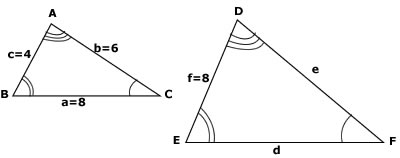
Solução:

Como os triângulos são semelhantes por hipótese, vem, pela razão de semelhança, que:

c = kf => k = c/f => k = 4/8 = 1/2

De forma análoga:

a = kd => 8 = (1/2)d => d = 16

b = ke => 6 =(1/2)e => e = 12

Propriedades

a) Reflexiva: Todo triângulo é semelhante a si próprio.

Propriedade Reflexiva

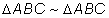
b) Simétrica: Se um triângulo é semelhante a um outro, este é semelhante ao primeiro.

Propriedade Simétrica

c) Transitiva: Se um triângulo é semelhante a um segundo e este é semelhante a um terceiro, então o primeiro é semelhante ao terceiro.

Propriedade Transitiva

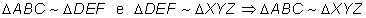
Teorema Fundamental

Se uma reta é paralela a um dos lados de um triângulo e intercepta os outros dois em pontos distintos, então o triângulo que ela determina é semelhante ao primeiro.

A demonstração do Teorema Fundamental é feita a partir do Teorema de Tales, que por sua vez pode ser demonstrado a partir dos critérios de semelhança definidos abaixo (fica como exercício).

Se um feixe de retas paralelas tem duas transversais, então a razão entre dois segmentos quaisquer de uma é igual à razão entre os segmentos correspondentes na outra.

Teorema de Tales

Demonstração do Teorema Fundamental:

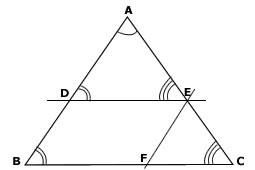
A demonstração da congruência dos ângulos dos triângulos ABC e ADE (figura abaixo) decorre do fato de que ângulos correspondentes determinados por duas paralelas são congruentes. Assim, o ângulo B é congruente ao D e o ângulo C é congruente ao E. Como o ângulo A é comum aos dois triângulos concluímos a primeira parte da demonstração.

Teorema Fundamental

Pelo Teorema de Tales temos que:

m(AD)/m(AB) = m(AE)/m(AC) [1]

Por E construímos a reta EF paralela a BD, conforme indicado na figura acima. Do paralelogramo BDEF temos que m(DE) = m(BF). E, novamente, pelo Teorema de Tales:

m(AE)/m(AC) = m(BF)/m(BC) => m(AE)/m(AC) = m(DE)/m(BC) [2]

De [1] e [2] vem que os lados homólogos são proporcionais, o que conclui a demonstração.

Observação: Nos termos do tipo m(AE), utlizados acima, imagine uma barra sobre AE para se ter a notação correta conforme indicado anteriormente.

Critérios de Semelhança de Triângulos

Critério AA => Ângulo-Ângulo: Se dois triângulos têm dois ângulos internos correspondentes congruentes, então os triângulos são semelhantes.

Demonstração:

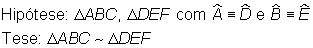Critério AA - DemonstraçãoNo caso dos dois triângulos serem congruentes, nada há a demonstrar, pois por definição de congruência os triângulos são necessariamente semelhantes. Suponhamos, então, como indicado na figura, o triângulo ABC maior que o triângulo DEF e construamos o triângulo AGH tal que a medida do lado AG seja igual à medida do lado DE, o ângulo G congruente ao ângulo E e H sobre o lado AC.

Critério AA - Demonstração

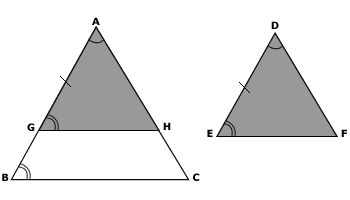
Além disso, como o ângulo A é congruente ao ângulo D, por hipótese, o triângulo AGH é congruente ao triângulo DEF (critério ALA da congruência entre triângulos) e portanto semelhantes.

Por outro lado, pelo Teorema Fundamental, temos que o triângulo AGH é semelhante ao triângulo ABC, já que o lado GH é paralelo ao lado BC. E, finalmente, como o triângulo ABC é semelhante ao triângulo AGH, e AGH, por sua vez, é semelhante a DEF, concluímos, pela propriedade transitiva, que o triângulo ABC é semelhante ao triângulo DEF.

As demonstrações dos demais critérios ficam como exercício.

Critério AAA => Ângulo-Ângulo-Ângulo: Se os ângulos de um triângulo forem respectivamente congruentes aos ângulos correspondentes de outro triângulo, então os triângulos são semelhantes.

Critério LAL => Lado-Ângulo-Lado: Se as medidas de dois dos lados de um triângulo são proporcionais aos homólogos do outro triângulo e os ângulos determinados por estes lados são congruentes, então os triângulos são semelhantes.

Critério LLL => Lado-Lado-Lado: Se as medidas dos lados de um triângulo são respectivamente proporcionais às medidas dos lados correspondentes de outro triângulo, então os triângulos são semelhantes.

Teorema de Pitágoras

Um triângulo é denominado retângulo se um de seus ângulos é reto, ou seja, tem 90 graus. O lado de maior medida é denominado hipotenusa (a) e os outros dois lados de catetos (b e c).

Teorema de Pitágoras

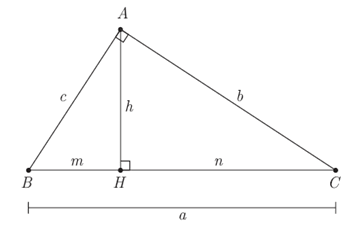
Pitágoras estabeleceu, então, em seu mais famoso teorema que: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos, i.e.:

a2 = b2 + c2

Para finalizar o artigo com chave de ouro vamos demonstrar o Teorema de Pitágoras com o uso dos critérios de semelhança.

Demonstração:

Observe que os triângulos ABH e ABC são semelhantes como decorrência do critério AA, uma vez que ambos possuem um ângulo reto e o ângulo B em comum. Daí tiramos a seguinte relação entre os lados homólogos:

c/a = m/c => c2 = a.m => c2 = a.(a – n) => c2 = a2 – an [1]

Pela mesma razão os triângulos AHC e ABC são semelhantes. Logo:

b/a = n/b => b2 = an [2]

Substituindo [2] em [1] vem que:

c2 = a2 – b2 => a2 = b2 + c2.

Nenhum artigo relacionado.