Neste artigo abordaremos os conceitos e propriedades de razões – Parte I – e em outro artigo, a ser publicado em breve, os conceitos e propriedades de proporções – Parte II.

Definições

A Razão entre dois números é o quociente ou a divisão do primeiro pelo segundo.

Em outras palavras, dados dois números a e b, b diferente de zero, a razão entre eles é definida pela expressão:

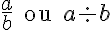
onde a, o primeiro número, ou numerador, é denominado o antecedente da razão e b, o segundo, ou denominador, o consequente da razão.

Formas comuns de leitura de uma razão a/b: “Razão de a para b”, “a está para b” ou “a para b”.

Exemplos:

1. A razão entre 28 e 4 é igual a 7 porque: 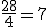. Note que o resultado dessa razão exprime que o antecedente contém sete vezes o consequente;

2. A razão entre 10 e 20 é igual a 1/2 porque: .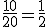

3. Em uma prova de 10 questões, você acertou 8. Nessas condições:

a) Qual a razão do número de seus acertos para o número total de questões do teste?

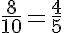, ou seja, de cada 5 questões você acertou 4.

b) Qual a razão do número de erros para o número total de questões do teste?

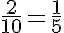, ou seja, de cada 5 questões você errou 1.

Razões Inversas: Duas razões são inversas quando o numerador da primeira é igual ao denominador da segunda e o denominador da primeira é igual ao numerador da segunda. De outra maneira, quando o antecedente de uma é igual ao consequente da outra e vice-versa.

Observe, no entanto, que uma razão cujo antecedente é igual a zero não possui inversa. Você sabe dizer por quê?

Exemplo: 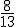e

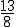
Como consequência dessa definição podemos concluir, facilmente, que o produto de duas razões inversas é igual a unidade. De fato multiplicando-se duas razões (frações) inversas quaisquer (a/b e b/a) obtemos utilizando-se das propriedades de multiplicação de frações que:

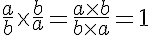
Observação: Até agora lidamos com exemplos onde está implícito que as grandezas são da mesma espécie e avaliadas na mesma unidade.

Antes de prosseguir e mostrar aonde queremos chegar com essa observação vamos primeiro estabelecer o conceito de grandeza.

Grandeza, nada mais é que uma relação numérica estabelecida com um objeto. Assim, a altura e o peso de uma pessoa, a área de um terreno, a quantidade de blogs, entre outros, são grandezas. Ou, em outras palavras, grandeza é tudo que você pode contar, medir, pesar, enfim, enumerar.

Bom! E para que isso tudo? Para chamar a atenção de que o cálculo de uma razão entre duas grandezas de mesma espécie (comprimento, por exemplo) não pode ser efetuado com unidades distintas (centímetro e metro). Exemplificando: para determinar a razão entre a minha altura 1,87 metros e a de Maria com 165 centímetros é necessário, antes, converter ambas para metro ou centímetro. A partir dessas considerações podemos, também, estabelecer a propriedade P1 a seguir.

Propriedades

P1. A razão de duas grandezas da mesma espécie, avaliadas com a mesma unidade, é igual à razão dos números que exprimem essas grandezas.

Nota: Chama-se valor de uma razão a fração irredutível que lhe é igual. Se q designar o valor de uma razão a/b, teremos:

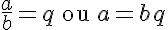
P2. Uma razão não se altera quando seus dois têrmos são multiplicados por um mesmo número.

Demonstração: Seja a/b uma razão. Precisamos demonstrar que, se multiplicarmos os seus dois termos por um número m, devemos obter:

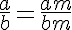
De fato, seja q o valor da razão. Pela definição vem que:

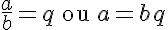
Multiplicando os dois membro da igualdade por m:

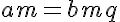
donde se tira, dividindo os dois membros por bm:

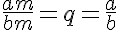
P3. O produto de duas razões é igual ao produto dos seus antecedentes dividido pelo produto de seus consequentes.

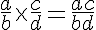
P4. O quociente de duas razões é igual ao produto da razão dividendo pela razão divisor invertida.

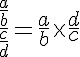
P5. Numa série de razões iguais, a soma dos antecedentes dividida pela soma dos consequentes dá uma razão igual a cada uma das razões dadas.

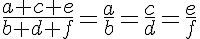
Referências:

Elementos de Aritmética, Curso Superior – Para o curso colegial e admissão às escolas superiores, do Irmão Isidoro Dumont, Coleção de Livros Didáticos F. T. D, publicado em 26/10/1945