O Viche tem recebido visitas a partir de pesquisas efetuadas no Google com o termo triângulo em função dos artigos publicados sobre Tecelagem Popular no Triângulo Mineiro. Assim, com o objetivo de atender esse indicativo presente nas estatísticas do blog passo a escrever sobre conceitos relacionados ao termo mencionado: mais especificamente sobre Semelhança entre Triângulos.
Antes, vamos definir o que é congruência entre triângulos.
Congruência entre Triângulos
Dois triângulos (ou de forma geral, duas figuras planas) são congruentes quando têm a mesma forma e as mesmas dimensões, ou seja, o mesmo tamanho.
Já a semelhança entre triângulos, objeto do artigo, aborda o conceito mais amplo onde se tem triângulos com a mesma forma, mas não necessariamente com o mesmo tamanho. Em outras palavras, congruência é um caso particular de semelhança entre triângulos no sentido de que se dois triângulos são congruentes necessariamente eles são semelhantes, mas o contrário não é verdadeiro, como você observará daqui em diante.
Definição de Semelhança entre Triângulos
Dizemos que dois triângulos são semelhantes se, e somente se, possuem seus três ângulos ordenadamente congruentes e os lados homólogos (homo = mesmo, logos = lugar) proporcionais.
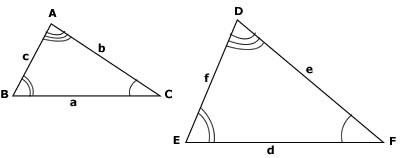
Traduzindo a definição em símbolos:
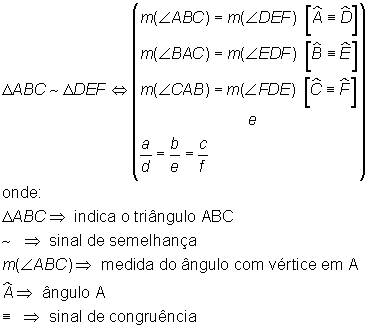
Observe que as três primeiras expressões entre os parêntesis indicam a congruência ordenada dos ângulos e a última a proporcionalidade dos lados homólogos.
Em bom português, podemos, ainda, definir a semelhança entre triângulos através da frase: dois triângulos são semelhantes se um pode ser obtido pela expansão uniforme do outro (caso deseje comprovar veja o programa em Java descrito abaixo).
Razão de Semelhança
Denominamos o número real k, que satisfaz as igualdades abaixo entre os lados homólogos, como a razão de semelhança dos triângulos:

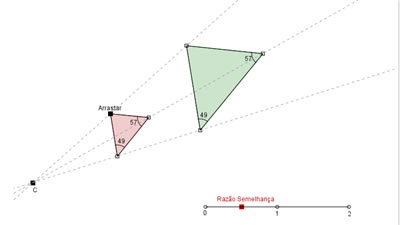
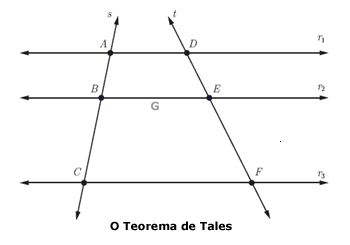
Para uma idéia melhor dos conceitos acima sugiro uma visita ao programa em Java de Karlos Gomes. A imagem inicial da página é apresentada a seguir, onde temos dois triângulos entre um feixe de três retas com origem no ponto C. Ao arrastar o triângulo rosa para cima ou para baixo, o ponto em vermelho no segmento de reta indica o valor da razão de semelhança correspondente. Ao colocar o triângulo rosa exatamente sobre o verde você observará que a razão de semelhança é igual a 1, como era de se esperar (você sabe dizer o significado deste fato?).
O único problema é que o programa demora a carregar. Tenha um pouco de paciência, e espere, vale a pena. Após, por favor, retorne a este artigo :-).
Exemplo
Dados os triângulos ABC e DEF semelhantes com as medidas dos lados indicadas abaixo, calcule as medidas dos lados e e d do segundo triângulo.
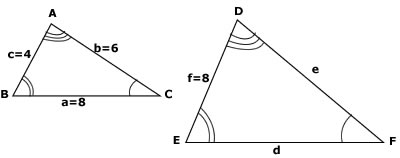
Solução:
Como os triângulos são semelhantes por hipótese, vem, pela razão de semelhança, que:
c = kf => k = c/f => k = 4/8 = 1/2
De forma análoga:
a = kd => 8 = (1/2)d => d = 16
b = ke => 6 =(1/2)e => e = 12
Propriedades
a) Reflexiva: Todo triângulo é semelhante a si próprio.
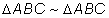
b) Simétrica: Se um triângulo é semelhante a um outro, este é semelhante ao primeiro.

c) Transitiva: Se um triângulo é semelhante a um segundo e este é semelhante a um terceiro, então o primeiro é semelhante ao terceiro.
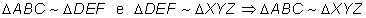
Teorema Fundamental
Se uma reta é paralela a um dos lados de um triângulo e intercepta os outros dois em pontos distintos, então o triângulo que ela determina é semelhante ao primeiro.
A demonstração do Teorema Fundamental é feita a partir do Teorema de Tales, que por sua vez pode ser demonstrado a partir dos critérios de semelhança definidos abaixo (fica como exercício).
Se um feixe de retas paralelas tem duas transversais, então a razão entre dois segmentos quaisquer de uma é igual à razão entre os segmentos correspondentes na outra.
Demonstração do Teorema Fundamental:
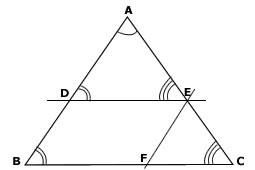
A demonstração da congruência dos ângulos dos triângulos ABC e ADE (figura abaixo) decorre do fato de que ângulos correspondentes determinados por duas paralelas são congruentes. Assim, o ângulo B é congruente ao D e o ângulo C é congruente ao E. Como o ângulo A é comum aos dois triângulos concluímos a primeira parte da demonstração.
Pelo Teorema de Tales temos que:
m(AD)/m(AB) = m(AE)/m(AC) [1]
Por E construímos a reta EF paralela a BD, conforme indicado na figura acima. Do paralelogramo BDEF temos que m(DE) = m(BF). E, novamente, pelo Teorema de Tales:
m(AE)/m(AC) = m(BF)/m(BC) => m(AE)/m(AC) = m(DE)/m(BC) [2]
De [1] e [2] vem que os lados homólogos são proporcionais, o que conclui a demonstração.
Observação: Nos termos do tipo m(AE), utlizados acima, imagine uma barra sobre AE para se ter a notação correta conforme indicado anteriormente.
Critérios de Semelhança de Triângulos
Critério AA => Ângulo-Ângulo: Se dois triângulos têm dois ângulos internos correspondentes congruentes, então os triângulos são semelhantes.
Demonstração:
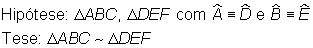 No caso dos dois triângulos serem congruentes, nada há a demonstrar, pois por definição de congruência os triângulos são necessariamente semelhantes. Suponhamos, então, como indicado na figura, o triângulo ABC maior que o triângulo DEF e construamos o triângulo AGH tal que a medida do lado AG seja igual à medida do lado DE, o ângulo G congruente ao ângulo E e H sobre o lado AC.
No caso dos dois triângulos serem congruentes, nada há a demonstrar, pois por definição de congruência os triângulos são necessariamente semelhantes. Suponhamos, então, como indicado na figura, o triângulo ABC maior que o triângulo DEF e construamos o triângulo AGH tal que a medida do lado AG seja igual à medida do lado DE, o ângulo G congruente ao ângulo E e H sobre o lado AC.
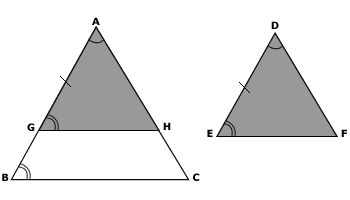
Além disso, como o ângulo A é congruente ao ângulo D, por hipótese, o triângulo AGH é congruente ao triângulo DEF (critério ALA da congruência entre triângulos) e portanto semelhantes.
Por outro lado, pelo Teorema Fundamental, temos que o triângulo AGH é semelhante ao triângulo ABC, já que o lado GH é paralelo ao lado BC. E, finalmente, como o triângulo ABC é semelhante ao triângulo AGH, e AGH, por sua vez, é semelhante a DEF, concluímos, pela propriedade transitiva, que o triângulo ABC é semelhante ao triângulo DEF.
As demonstrações dos demais critérios ficam como exercício.
Critério AAA => Ângulo-Ângulo-Ângulo: Se os ângulos de um triângulo forem respectivamente congruentes aos ângulos correspondentes de outro triângulo, então os triângulos são semelhantes.
Critério LAL => Lado-Ângulo-Lado: Se as medidas de dois dos lados de um triângulo são proporcionais aos homólogos do outro triângulo e os ângulos determinados por estes lados são congruentes, então os triângulos são semelhantes.
Critério LLL => Lado-Lado-Lado: Se as medidas dos lados de um triângulo são respectivamente proporcionais às medidas dos lados correspondentes de outro triângulo, então os triângulos são semelhantes.
Teorema de Pitágoras
Um triângulo é denominado retângulo se um de seus ângulos é reto, ou seja, tem 90 graus. O lado de maior medida é denominado hipotenusa (a) e os outros dois lados de catetos (b e c).
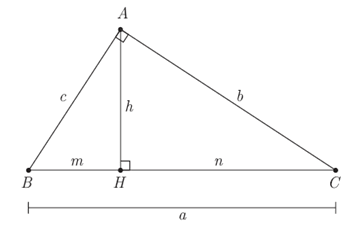
Pitágoras estabeleceu, então, em seu mais famoso teorema que: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos, i.e.:
a2 = b2 + c2
Para finalizar o artigo com chave de ouro vamos demonstrar o Teorema de Pitágoras com o uso dos critérios de semelhança.
Demonstração:
Observe que os triângulos ABH e ABC são semelhantes como decorrência do critério AA, uma vez que ambos possuem um ângulo reto e o ângulo B em comum. Daí tiramos a seguinte relação entre os lados homólogos:
c/a = m/c => c2 = a.m => c2 = a.(a – n) => c2 = a2 – an [1]
Pela mesma razão os triângulos AHC e ABC são semelhantes. Logo:
b/a = n/b => b2 = an [2]
Substituindo [2] em [1] vem que:
c2 = a2 – b2 => a2 = b2 + c2.



fev 05, 2011 @ 15:01:57
Poow mutii boom. !
Vlw aii Conseguii entender i Fazeer meeu deever =D
*—*
fev 02, 2011 @ 20:54:50
me ajudou a fazer uma pesquisa da escola………………….obrigada
jan 02, 2011 @ 11:46:00
ihh facinho e não é questão de idade nem nada na verdade acho que esse assunto era pra dar mais cedo pois com 12 anos john nash fazia esperiemntos cientificos no quarto dele ‘-‘
dez 16, 2010 @ 19:49:05
muito dificil e n enendi nada!!!
dez 11, 2010 @ 23:08:58
Gostei muitissímo desse site pq me ajudou bastante
dez 08, 2010 @ 22:25:02
AH! FANTÁSTICO O MUNDO DA MATÉMATICA , O ASSUNTO É DIFICIL NO COMEÇO MAS DEPOIS AGENTE APRENDE E VÊ QUE É FACÍL E DEPOIS PEGA A PRATICÁ!PELO MENOS PRA MIN FOI ASSIM! MAS QUEM ACABA DEIXANDO O ASSUNTO DIFICIL SÃO NOISS MESMOS!!
dez 06, 2010 @ 17:51:23
na era nada disto qe eu tava a procura
mt obrigado a todos
dez 01, 2010 @ 21:02:47
:OOOO com 13 anos aprender isso é tenso :OOO
nov 22, 2010 @ 11:22:40
teorema de tales é dificil!!!!!!!!!!!
nov 22, 2010 @ 11:20:45
eu gostei,mas é um pouco dificil!!!
teorema de tales,eu conheci atraves do professor de matemática
e eu fui me enteressando pelo teorema de tales.
nov 19, 2010 @ 20:05:17
Muito dificil, epra quem não sabe isso se aprende no 8ºAno (7°série)
nov 16, 2010 @ 08:49:31
adoremos!!
nov 13, 2010 @ 17:50:23
ñ gostei porque é muito dificiu de fazer!
esse tal de semelhanças entre triângulos…..
nov 12, 2010 @ 17:54:50
.amei muito bommm????????????????????
nov 11, 2010 @ 12:31:55
Exatamente o que eu precisava para montar minha aula, achei que ficou bem explicado.
So precisava lembrar em que serie se ve isso…
nov 09, 2010 @ 21:27:24
heeei , coonseguii agoora ..
deeu p. enterdeer um pooucoo seei qe os nuumeroos de dentro do triangulo somados tem que dar o resultado de 180 sempre =]
nov 09, 2010 @ 16:36:00
Eu nao sei como que se faz angulos e triangulos e eu queria muito aprender
nov 06, 2010 @ 11:55:32
eu adorei tudo,
o q eu presisava estava aqui
kis kis kis xauuu ate a proxima
beijos
nov 04, 2010 @ 23:01:13
Intão… Num Entendi Nada…
Só Copiei Pra Entregar Pra Prof… ;s
Mesmo Assim, Ta bem Explicado, Só Pros Estudientes…
nov 04, 2010 @ 22:24:21
Pooooooxa .,
too mtooo triiste nãao entende neeckiit catiibiriiba .
Mee expliiica gnt ‘ :[
nov 02, 2010 @ 21:34:07
POW mAN Q ISSO CARA.TEM NADA DO Q EU PROCURO AI ..
out 29, 2010 @ 15:24:12
muito dificil
out 29, 2010 @ 15:23:26
não entendi boufas
out 26, 2010 @ 17:44:10
gostei muito facil
out 24, 2010 @ 15:08:13
gostei do artigo intereçante mais acho que pudiamos colocar mais figuras de triangulos
out 20, 2010 @ 23:17:39
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
Q mizeraaaa isso pra mim e outra lingua num entendo essa mizera nem kum krai affz
Alguem pode me ajudar ??? :D (yy’
out 19, 2010 @ 17:38:34
ameiiiiiii me ajudou muiito no trabalho tudo que eu deveria pesquisar eu achei.obg povo bjokas..
out 13, 2010 @ 17:09:03
tenhu grades dificuldades e estou na oitava serie!o que deveria fazer para molhorar meu aprendizado?
out 12, 2010 @ 13:34:15
Mto bom esse conteudo , poderia ter uns exercicios para resolver .xD
set 25, 2010 @ 13:14:29
eu gostaria de saber se a razão é dada pelo triangulo menor /triangulo menor, se pode ser o contrario, se ao aplicar o criterio angulo angulo eu posso fazer a razâo so do triangulo formado no grande ou se eu posso fazer dos lados q sobraram do triangulo grande pelo triangulo menor.
e o conteudo é ótimo, parabéns
set 23, 2010 @ 11:09:20
nossa este projeto me ajudou de mais
Conseguir tudo que procurava…
set 14, 2010 @ 14:33:22
man explica diretio isso ai -.-
ago 27, 2010 @ 09:26:22
muito bom o contudo continuem assim
okkk muito obrigada vcs mim ajudaram
d++++…………………………..
ago 19, 2010 @ 19:25:38
eu de vo essa a vcs!brigadão.depois dessa ajudinha fika mais fáácil tira um dez em matemática!rsrsrs…kkkkkkkkkk
brigadão mesmo!bjus
quando prescisar jáá seiii onde procurar.bjus
ago 19, 2010 @ 19:22:38
eu ameiiii emcontrei exatamente oq queria obrigadoooooOH.BJUS
continuem assim,!!!enovando sempre!bjus
ago 15, 2010 @ 23:59:10
eu queria saber se tem como eu colocar as perguntas que eu quero saber as respostas pra vcs responderem na hora ??
jul 21, 2010 @ 19:29:40
esse exercicios e muito massa cara explica +ou- mais é massa!!!!!!!!
kkkk
jul 02, 2010 @ 23:21:47
Gente que Legal esse site me ajudo muitíssimo mesmo eu assim amei porque estava pesquisando sobre semelhança para a pesquisa da escola e isso ajudo muito!!
Agora é só espera pra tirar um 10 em geometria rsrsrs…
Obrigado e continuem postando mas para que sempre que a gente precisar já saber a onde achar
jun 04, 2010 @ 00:02:02
ameiii….nao deixem este site sem atualizaçoes gente …ele é um maximo…eu faço matematica e as vezess quase morro …. muito bommm.valeu a ajuda
maio 24, 2010 @ 15:48:25
Mto bom
vlw
vo fica devenu essa!
XD
Tweets that mention Semelhança Entre Triângulos -- Topsy.com
maio 07, 2010 @ 00:01:29
[…] This post was mentioned on Twitter by Giulia Yamamoto. Giulia Yamamoto said: @feelingthis http://www.blogviche.com.br/2006/12/15/semelhanca-entre-triangulos/ […]
abr 27, 2010 @ 14:27:32
Preciso de um comentário mais resumido sobre isso alguem poderia me ajudar????????????? : )
abr 26, 2010 @ 21:58:17
MUITOOOOOOOOO BOMMM… me achudou bastante
abr 24, 2010 @ 16:06:34
2x-(-18x)+53-23=180
2x+18x=-53+23+180
20x=150
x=150/20
x=7,5
tah ai!Espero ter te ajudado
abr 16, 2010 @ 08:26:05
adorei continuem assim
mar 26, 2010 @ 18:38:54
muito bom o conteúdo…
mar 26, 2010 @ 00:18:45
preciso que me ajudem a resolver , 2x-(-18x)+53-23=180
mar 15, 2010 @ 19:54:46
tava aqui na net procurandoo semelhança geral de triângulos para a pesquisa de geometria, ameii o site tudoo q eu precisava estava aqui.
continuem sempre assim, inovem tbm e procurem mandar noviis pra o e-mail de kda um dos comentaristas sobre os detalhges do site. As inovações que estarão ocorrendo no decorrer do ano.
um grande beijo e vllw *—–*
dez 17, 2009 @ 17:55:55
Eu não. ¬¬’
dez 15, 2009 @ 15:05:52
amei….
consegui tudo oque eu queria…