Para complementar o artigo escrito sobre Conjuntos Numéricos iremos abordar agora o conceito de intervalo na reta real R. Ou seja, dos subconjuntos de R que satisfazem à seguinte propriedade:
se x e y pertencem a I C R, x ≤ y, então para todo z tal que x ≤ z ≤ y, então z pertence a I
Sem entrar em detalhes, e apenas como informação adicional, a propriedade estabelece que os intervalos são subconjuntos conexos de R, como também o é o próprio R, ou subconjuntos contínuos de R.
Em forma de conjunto a propriedade acima pode ser escrita como:
I = {z ε R | x ≤ z ≤ y}
Os intervalos podem ser classificados por suas características topológicas – abertos, fechados e semi abertos (fechados ou abertos à esquerda ou à direita) – e por suas características métricas – comprimento nulo, finito não nulo ou infinito.
Notação em símbolos de um intervalo
Habitualmente se utilizam os colchetes – “[” e “]” – para indicar que um dos extremos do intervalo é parte deste intervalo e os parênteses – “(” e “)” – ou, também, os colchetes invertidos – “]” e “[” para indicar o contrário.
Assim, por exemplo, dados a e b números reais, com a ≤ b, o intervalo I = (a,b] = ]a,b] representa o conjunto dos x ε R, tal que a < x ≤ b. Note que a não faz parte do intervalo.
Representação de um intervalo na reta real
Um intervalo é representado na reta real utilizando-se de uma pequena “bolinha vazia” para indicar que um dos pontos extremos não pertence ao intervalo e de uma “bolinha cheia” para indicar que o ponto extremo pertence.
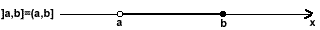
Tipos de Intervalos
Dados a e b números reais, com a ≤ b, x pertencente ao intervalo e c o seu comprimento, podemos classificar os intervalos como:
a) Intervalo Fechado de comprimento finito c = b – a:
[a,b] = {x ε R | a ≤ x ≤ b}
b) Intervalo fechado à esquerda e aberto à direita de comprimento finito c = b – a:
[a,b[ = [a,b) = {x ε R | a ≤ x < b}
c) Intervalo aberto à esquerda e fechado à direita de comprimento finito c = b – a:
(a,b] = ]a,b] = {x ε R | a < x ≤ b}
d) Intervalo aberto de comprimento finito c = b – a:
]a,b[ = (a,b) = {x ε R | a < x < b}
e) Intervalo aberto à direita de comprimento infinito:
]-∞,b[ = (-∞,b) = {x ε R | x < b}
f) Intervalo fechado à direita de comprimento infinito:
]-∞,b] = (-∞,b] = {x ε R | x ≤ b}
g) Intervalo fechado à esquerda de comprimento infinito:
[a,+∞) = [a,+∞[ = {x ε R | a ≤ x}
h) Intervalo aberto à esquerda de comprimento infinito:
]a,+∞[ = (a,+∞) = {x ε R | x > a}
i) Intervalo aberto de comprimento infinito:
]-∞,+∞[ = (-∞,+∞) = R
j) Intervalo fechado de comprimento nulo:
Como o comprimento é nulo e o intervalo fechado, então a = b e esse intervalo corresponde ao conjunto unitário {a}, isto é, a um ponto da reta real.
Concluo a classificação dos intervalos com a seguinte pergunta para vocês: E o intervalo vazio como seria definido?
União e Intersecção de Intervalos
Como intervalos são conjuntos é natural que as operações mencionadas possam ser realizadas. E, trata-se de um procedimento muito comum na resolução de alguns problemas.
E a maneira mais fácil e intuitiva de realizar essas operações é através da representação gráfica dos intervalos envolvidos. Vamos à um exemplo prático de como efetuar tais operações.
Sejam A = [-1,6] = {x ε R | -1 ≤ x ≤ 6} e B = (1,+∞) = {x ε R | x > 1} dois intervalos e vamos determinar A U B e A ∩ B.
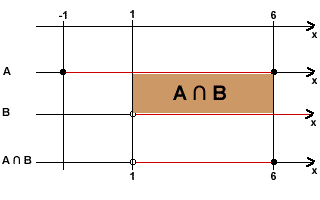
Primeiramente, marcamos todos os pontos que são extremos ou origens dos intervalos em uma mesma reta. Em seguida, abaixo dessa reta, traçamos os intervalos que representam graficamente os conjuntos A e B. E, por fim, é só utilizar a definição de união e intersecção para determinar os trechos que estão em pelo menos um intervalo e os trechos comuns aos dois intervalos, respectivamente. Veja a solução de A ∩ B na figura a seguir e de onde é também facilmente observado o resultado de A U B:
A ∩ B = {x ε R | 1 < x ≤ 6} e A U B = {x ε R | -1 ≤ x}



dez 04, 2017 @ 17:15:06
pORAAAA MELHOR EXPLICAÇÃO DA INTERNET HAAHA
abr 24, 2013 @ 16:33:55
tirando q váaaaarios ai precisam de aula de português… mas enfim, a explicação é boa, se meu professor falasse assim eu tinha entendido há anos
abr 01, 2013 @ 09:21:41
eu nao entendi a interseccao dos intervalos da reta so.
mar 06, 2013 @ 09:33:11
por favor me ajudem 1: conjuto de numeros reais e a reta numerica real – teoria e 3 exercicios resolvidos 2:intervalos reais – teoria e 3 exercicios resolvidos 3: funcoes e graficos- teoria e 3 exercicios resolvidos
set 26, 2012 @ 16:59:43
AAAAAAAAAAAAA! Eu não sei de nada!
ago 16, 2012 @ 21:08:06
amanhã prova de matemática e não sei de nada:(
jul 25, 2012 @ 22:08:09
nao entendi foi porra nenhuma esse carai e difice q so
abr 25, 2012 @ 04:30:59
realmente essa ideia de estudar virtualmente e uma maravilha força
mar 11, 2012 @ 15:49:24
No último tópico a formula deveria incluir o intervalo de 1 a + infinito e não o contrário
mar 11, 2012 @ 15:50:05
*A U B
mar 11, 2012 @ 14:35:12
Por favor, como expressar esse intervalo usando a representação com chaves? (-raiz de 3, 2 ]
Obrigada
fev 29, 2012 @ 08:36:40
adorei as respostass..
nov 30, 2011 @ 10:15:52
deu pra entende
show
ago 12, 2011 @ 19:41:12
gostaria que falassem mais sobre intervalos infinitos pois neste texto não são tão explicitos como deveriam ser,mas deu para ter uma noção do assunto.
ago 06, 2011 @ 19:34:28
não consegui encontrar em livro nenhum a representação de resolver intervalos reais na reta. minha dif iculdade e a-b, b-c c-a c-R na representação da reta real. Um dais minhas diculdade é saber quando devemos inverter o a bolinha aberta para feichada, feichado para aberto.
jul 06, 2011 @ 20:31:48
alguem pode me da 1 allinha extra estou presisando urgente relp
jun 22, 2011 @ 16:22:05
Eu não entendo “picas” de intervalos numéricos, alguém me ajude.
Observação: AJUDA É URGENTE!
jul 10, 2012 @ 11:10:16
faça vc msm
jun 06, 2011 @ 13:24:14
AMANHATENHO TESTE DEMATEMATICA E NAO SEINADA !
jul 06, 2011 @ 20:30:01
Eu tambem tenho prova amanhã e ñ sei nada
set 13, 2011 @ 16:32:43
eu posso te ajudar. add meu e-mail que agente conversa
maio 01, 2012 @ 11:52:39
nao precisa ajudar viuuuuuuuuuuuu
maio 22, 2011 @ 13:25:47
mi ajude por favor segunda-feira tem um aprova de matematica orrivel.
maio 26, 2011 @ 15:41:24
matematica e orrivel mas eu acho que ate aprendi alguma coisa!
ago 17, 2012 @ 11:30:53
Acho que você precisa de ajuda em Português também, porque né..
maio 19, 2011 @ 15:41:31
AIII MII AJUDOU MUITO TBM BOA SORTE AII GNETE
maio 10, 2011 @ 18:00:56
essa aula foi fantástica eu estou super entendendo matemática, valeu
maio 10, 2011 @ 17:56:19
essa aula foi demais.depois que li melhorei nas minhas provas
maio 10, 2011 @ 11:40:06
alguem me ajude não sei nada?socorooooooooooooo
abr 15, 2011 @ 23:15:33
Esse site me ajudou, mais o livro MATEMÁTICA DANTE VOLUME ÚNICO me ajudou muito mais espero que ajudem vcs tambem boa sorte bjs
abr 11, 2011 @ 13:10:09
estou desisperada hj tem uma prova pra fazer hj de matematica e ñ sei fazer reta real me ajudem…
abr 09, 2011 @ 14:11:42
Ola! O Professor me deu uma questao de intervalo que dizia A = ]-2,1[ , e pedia para calcula A, so que tinha uma barrinha em cima do A alguem me explica isso __
A
maio 27, 2011 @ 16:21:24
oi tudo bem
abr 07, 2011 @ 19:22:21
é muito ruim esse asunto mas deu pra entender um pouco!!!!!!!!!!!!!!!!
jan 11, 2012 @ 15:56:01
A explicação é boa, mas faltou mais exempos.