Frações Irracionais e Racionalização
maio 21st, 2006
O objetivo é apresentar as principais técnicas utilizadas na racionalização de denominadores de frações irracionais, uma vez que não é possível estabelecer uma regra geral face à infinidade de formas que esses denominadores podem assumir.
Para que o entendimento seja mais efetivo é imprescindível o conhecimento das propriedades de Radiciação e Potenciação, dentre outros conceitos que serão apresentados mas não demonstrados, por fugirem ao escopo da matéria.
O assunto está sendo tratado em decorrência do resultado da pesquisa feita no Blog, em que obteve a segunda colocação entre os temas propostos (11 votos). Maiores detalhes podem ser obtidos através do link Consultar Pesquisas na barra lateral de navegação.
FRAÇÕES IRRACIONAIS
Definição
Fração irracional é a que tem pelo menos um termo, o numerador ou o denominador, irracional ou sob radical.
Exemplos:
RACIONALIZAÇÃO DOS DENOMINADORES DE FRAÇÕES IRRACIONAIS
As técnicas a serem explicitadas considerarão, claro, as frações irracionais dos tipos indicados nos exemplos b) e c) acima.
Tem grande importância no processo de racionalização a seguinte propriedade das frações: Uma fração não se altera quando o numerador e o denominador são multiplicados pelo mesmo número diferente de zero.
Definições
Racionalização dos denominadores irracionais de uma fração irracional é a operação que tem por finalidade transformá-la em um número inteiro ou em uma fração equivalente com denominador racional.
Exemplos
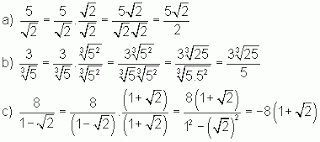
Fator racionalizante de uma expressão irracional é uma outra expressão, também irracional, em que o produto entre elas resulta em uma expressão sem radical, ou seja, que a torne uma expressão racional.
Para que o significado de fator racionalizante seja melhor entendido nada como alguns exemplos:
Observe que nos exemplos da definição de Racionalização dos denominadores irracionais foi utilizado o conceito de fator racionalizante.
Produtos Notáveis
Os produtos notáveis, ou derivados deles, têm um papel importante na racionalização de denominadores de frações irracionais. Por isso, faço um parêntesis para, antes de colocar as técnicas, definir alguns dos mais utilizados:
1) a2 – b2 = (a + b)(a – b)
2) a3 + b3 = (a + b)(a2 – ab + b2)
3) a3 – b3 = (a – b)(a2 + ab + b2)
Note que no exemplo b) acima foi utilizado o produto notável definido em 1) e no c) o definido em 2).
Técnicas ou Regras de Racionalização Mais Frequentes
T1. Frações irracionais do tipo:
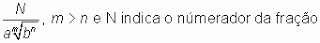
têm como fator racionalizante:
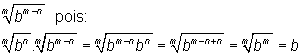
Exemplos:
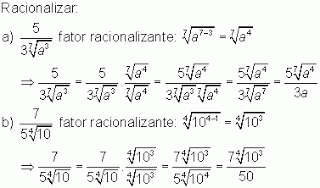
T2. Frações irracionais que têm no denominador um binômio de termos que são do mesmo índice 2 (raízes quadradas):
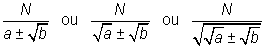
têm como fatores racionalizantes:
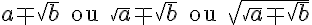
respectivamente.
Demonstração do segundo tipo:
Bem simples, basta somente usar o produto notável definido em 1) acima:
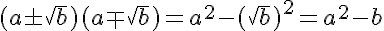
A demonstração dos demais seguem raciocínio semelhante e ficam como exercício.
Exemplos
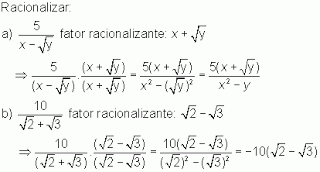
T3. Frações irracionais que têm no denominador um polinômio de termos que são do mesmo índice 2 (raízes quadradas):
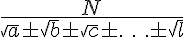
A idéia é fazer recair no caso anterior mediante uma adequada associação de termos. Para ilustrar, é apresentada a demonstração para n = 3. Você observará que a racionalização necessitará de dois fatores racionalizantes.
Demonstração:
Exemplo:
T4. Frações irracionais que têm no denominador um binômio de termos que são do mesmo índice 3 (raízes cúbicas):
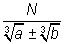
têm como fator racionalizante:
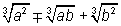
A demonstração já foi feita no exemplo c) da definição de fator racionalizante e é consequência dos produtos notáveis 2) e 3) definidos anteriormente.
Referências:
- Abecedário da Álgebra (Volume 1 – Ciclo Ginasial), Darcy Leal de Menezes, Rio de Janeiro, Departamento de Imprensa Nacional, primeira edição, 1959;
- Praticando Matemática, Álvaro Andrini, São Paulo, Editora do Brasil S/A.
Artigos Relacionados:
- Frações: Operações – Parte III
- Frações: Redução – Parte II
- Frações – Parte I
- Conjuntos Numéricos
- O VICHE Agora Tem Pesquisa (Enquete)
Posts relacionados trazidos a você pelo Yet Another Related Posts Plugin.
Categorias: Matemática,Técnico
Imprima este artigo
Envie este artigo para um(a) amigo(a)
101.224 views
122 Comentários Adicione o seu
1. Moacir Borges Pereira&hellip | maio 31st, 2006 at 14:14:22
Parabéns pelo site , muito bom !
2. Deise Prospero&hellip | maio 31st, 2006 at 19:37:28
muito bom o site , e minha pergunta sobre a prop 3?
3. Newton de Góes Horta&hellip | junho 1st, 2006 at 08:33:53
Denise,
Respondi à sua pergunta, por E-Mail, no mesmo dia do comentário anterior feito no artigo sobre Radiciação, com outra pergunta.
A propriedade P3 estabelece uma relação de igualdade e não cabe demonstrar se ela é ou não irracional.
Agora, se o que você deseja saber é se os membros da igualdade são ou não irracional vai depender do valor de a, b e n.
Por exemplo se a = 1, b = 16 e n = 2 o resultado é 1/4, e portanto racional. No artigo sobre Radiciação (comentário 22) tem um outro exemplo onde se tem como resultado uma fração irracional.
4. GIOVANI&hellip | junho 12th, 2006 at 20:18:12
mto bom. vc esta de parabens pelo seu site. apesar de n mostra o q eu devidamente estava procurando.
5. noemia&hellip | junho 17th, 2006 at 21:53:33
Muito bomo seu site, parabéns está ajudando muita gente. É bom ter gente que sabe compartilhar
6. Luis&hellip | junho 22nd, 2006 at 15:16:16
Didática muito boa. Abraços!
7. Diléia da Silva Brun&hellip | julho 17th, 2006 at 21:17:11
Teria como você me responder, utilizando a teoria lógica bicondicional, teoria do absurdo, que raiz de 2 é irracional?
Desde já agradeço! se não tiver resposta poderia me indicar alguem que me ajudasse?
Espero retorno!!
8. Francielli Reguengo Peres&hellip | julho 23rd, 2006 at 21:32:20
Oi, a minha dúvida é o seguinte, na soma da radiação, eu somei o valor que eu tirei da raiz quadrada. Gostaria de saber se é assim o certo ou não?
Ficarei muito grata.
Adorei o seu site.
Espero retorno!!
9. ana carolina&hellip | agosto 8th, 2006 at 09:54:58
oi gostei muito do seu site mais eu queria que tivesse uma calculadora automatica para poder fazer a soma seria uma ótima idéia né?
sem querer dar paupites mais porque voce nao poem uma .
seu sit ia ficar mais bonito e mais facil de poder entender não é verdade?
então acho que tem como melhorar um poquinho mais o seu site ta?
abraços e espero uma resposta de serta fração 58 por 72 simplificando-a obrigada e espero resposta mil beijos xau
10. ana carolina&hellip | agosto 8th, 2006 at 10:01:09
oi sou eu de novo mais que xato né?
me desculpe pelo que falei pois na verdade o seu site é muito bom e ja consegui achar a fração de 58 por 72 simplificando ta? mais porfavor me mande uma resposta do meu comentario sobre o seu site pois eu nunca recebo e-mail e seria ótimo se recebece um de vez enquando mais eu acho que estou sendo uma chatona né então vo embora e vo para de encher o seu saco ta? agora e verdade e pense um pouco sobre a calculadora automatica que eu disse pois ficaria mais facil da pessoa entender né mais no fundo sei que voce concorda comigo né? agora beijos e xau e vese me manda e-mail como eu dise ta? só tenho 10 anos e parece que todo mundo me odeia ta? beijos xau
11. ana carolina&hellip | agosto 8th, 2006 at 10:01:54
ai to sendo xata e insuportavel agora eu paro ta? xau
12. ana carolina&hellip | agosto 9th, 2006 at 08:54:20
oi sou eu de novo tudo bem?
gostei da menssagem que voce me mandou e gostei muito do seu site esera que é possivel nós converssarmos de e-mail por e-mail?
sem querer ser chata.
espero uma resposta xau
13. Ruth António da Costa Zi&hellip | agosto 11th, 2006 at 11:43:50
O vosso site e muito interessante gostei muito mais ainda vou pesquisar com mais calma.gostaria que se tivesse duvidas consultar o vosso site
14. Assis cesar mateus&hellip | setembro 5th, 2006 at 08:47:54
adorei o vosso e bué fixe
15. thammyres dinarte&hellip | setembro 20th, 2006 at 14:14:20
oi seu site ta bacana, pena q eu n axei bem o q qria, eu tava procurando um assunto mais detalhado sobre produtos notaveis,e infelizment aki n encontrei…
16. Jéssica&hellip | outubro 7th, 2006 at 11:36:51
seu site é muito legal
estou querendo uns exercicios para fazer de bháskara(simples),
racionalização e de incompleta
se puder me ajudar fico grata
beijos
17. lucas pacher&hellip | novembro 29th, 2006 at 13:27:57
gostei muito mas eu gostaria de excícios
18. maria de fatima&hellip | fevereiro 21st, 2007 at 15:57:58
obrigada, por essa explicação de racionalização, como mim ajudou , pois nunca entendia isso muito bem.
beijos
19. LUIZA FERNANDA PEREIRA GO&hellip | março 13th, 2007 at 19:40:59
CARAMBA!! ADOREI ESSE SITE;ELE NOS AJUDA A ESCLARECER DUVIDAS;E ALEM DE ENCAIXAR EM FUNÇÃO DE “PROFESSOR”. MUITO OBRIGADA MESMO.
20. Marcela Aparecida Assolar&hellip | março 17th, 2007 at 11:11:40
Olá para todos!!!!
Gostaria que me ajudassem a resolver esse problema de P.A., Por favor!!
Determine o terceiro termo de uma P.A, sabendo que o primeiro termo é igual a 3 e a razão é igual a -2.
Por favor, me ajudem pois eu estou estudando para prova que vai ser dia 19/03/07.
Obrigada!!!!!!
Até +
21. Murilo&hellip | março 20th, 2007 at 15:43:10
era sobre a racionalização q estava buscando +não consegui pq meu professor passou assim tem 2 raiz de 6 e ai multiplica o 6 e da 36 depois fica 2 raiz de 6 sobre 36 e depois corta só que aqui diz coisa diferente + msm assim muito obrigado .
22. Elson de Andrade&hellip | março 26th, 2007 at 21:12:46
O site é muito bom, está me ajundado muito.
Há duas coisas que gosto sei muito pouco as duas coisas e por isso, acredito que gostar talvez seja a inqietude da busca aprendemos a gostar das coisas que desejamos saber fazer.
Gosto de Matemática e Português
23. camila&hellip | abril 15th, 2007 at 13:34:17
Sinto muito mas eu não achei nada
24. julia&hellip | abril 16th, 2007 at 11:31:24
nao entendi nada!!!
25. rafa&hellip | abril 16th, 2007 at 11:37:39
alguem pode me explicar?
26. valdomz&hellip | abril 24th, 2007 at 10:24:04
ta ae… gostei da ideia do seu site. tou cursando matemática e acho que essa é uma boa forma de ajudar a quem tem dúvidas nessa área (pena que nao é todo mundo que tem acesso a net mas pra quem tem, fica valendo)…
abraço…
valdomz a.k.a. karap!nha
fica na paz
27. adeilson&hellip | maio 8th, 2007 at 19:37:10
Adorei as explicaçoes,sao muito bem detalhadas,razao pela qual eu aprendi com muita facilidade!!!!!
28. graziele&hellip | maio 9th, 2007 at 14:55:56
gostei
contrinuem assim
beijos!!!!
29. Helga Maia&hellip | maio 14th, 2007 at 11:16:18
Oi, parabéns pelo site, é ótimo…
Tem alguma regra pra encontrar o fator racionalizante (assim não seria preciso ficar guardando várias formas diferentes de racionalizar)?
Se puder mandar a resposta pra mim por e-mail, ficarei grata!!!
Ou então a indicação de algum site onde possa encontrar isso…
Bjossssss,
Obrogada.
30. larissa&hellip | maio 15th, 2007 at 12:38:47
afff…
não gostei do site pq não encontrei o que queria..
ai nao gosteiii
31. larissa&hellip | maio 15th, 2007 at 12:42:54
tá gostei do site
32. Aline&hellip | maio 22nd, 2007 at 09:58:46
site bom + mto resumido =/
33. michelle&hellip | maio 24th, 2007 at 10:57:32
aah, amei as explicações são bem faceis de intender e tirou muitas duvidas minhas !
beijo :*
34. Elizeu Martins&hellip | junho 4th, 2007 at 12:59:24
gostaria muito q tivesse exemplos de fração sobre fração, não consigo achar ex: 1/4/1
35. Taciano S Zimmermann&hellip | junho 14th, 2007 at 20:00:19
queria racionalizar:
2 / 2 + ³√2
36. antonio gomes lacerda&hellip | junho 16th, 2007 at 17:03:54
Voce saberia me responder filosoficamente porque a/b com b diferente de zero é uma razao? O por quê da palavra razao?
37. victor&hellip | junho 19th, 2007 at 19:27:12
1
________
raiz cubica d 2 menos 1
quem poder resolver para mim , por favor mand parab meu e-mail
38. adair rodrigues belmonte&hellip | junho 27th, 2007 at 20:05:08
muito legal foi otimo pesquisar por aqui
39. saulo felix&hellip | junho 30th, 2007 at 16:03:44
O site é bom , más a procura maior pelo conjunto dos irracionais tende ao campo de novos jogos e praticas pedagogicas para seu aprendizado
40. adair rodrigues belmonte&hellip | julho 31st, 2007 at 22:40:18
gostaria de receber informações de como se resolve numeros com raizes
41. kadu&hellip | agosto 5th, 2007 at 19:18:29
como eu simplifico essa conta?
4+raiz de 12/por 2
42. Gumer Hango&hellip | setembro 3rd, 2007 at 19:30:01
Qro por favor se poderem q me enviem alguns exercicios acerca d radicais de radicais
43. Graciliene Ceres&hellip | setembro 15th, 2007 at 18:12:40
Olha adorei teu site… parabéns… tira nossas dúvidas na hora!!! Muito obrigada!!!
44. una&hellip | outubro 18th, 2007 at 14:55:02
afff… esta muito resumidoo… e nao ha exemplo..
45. Heldemar Rebouças&hellip | novembro 17th, 2007 at 18:19:26
parabéns pelo site ajudou bastante.
serve como prova que a net tb pode ser usado muito bem.
abraços
46. felipe&hellip | novembro 28th, 2007 at 11:38:26
eu gostei mas podia de mas coisas todos
47. >.&hellip | dezembro 11th, 2007 at 17:40:17
Num entendi nada uhAUshUA
48. Osvaldo Rosa de Moura&hellip | janeiro 9th, 2008 at 22:48:28
Seu site é DEZ. Gostei muito
49. zacarias zuzi goma&hellip | janeiro 24th, 2008 at 12:44:56
eu gostei muito deste saite porq eu quero aprender nele.
50. Amanda&hellip | fevereiro 12th, 2008 at 14:13:15
Olá…
Gostei muito do site, encontrei exatamente o que eu estava procurando e fica aqui uma sugestão: talvez as contas devessem ser melhor explicadas e não somente mostradas, desse modo a compreensão seria melhor!
Obrigada pela atenção!!!
51. Domingos&hellip | março 10th, 2008 at 21:28:20
Excelente !! Guia rápido de bolso.
52. Érika&hellip | março 16th, 2008 at 21:40:47
Bom, eu adoorei a explicacação,poois eu estudando isso na 8 série, e era tudo que eu queria para poder intender melhor o assunto ^^ !
Obriigada ;D
beeijo ;*
53. , Matheus .&hellip | março 17th, 2008 at 14:42:53
Massa (y.
;)
54. Karine e Daíse&hellip | abril 4th, 2008 at 14:44:25
Esse assunto e muito interesante por que com essa pesquisa nós aprendemos mais.
55. laegila&hellip | abril 5th, 2008 at 17:17:51
parabens pelo site o conteudo e muito bom e o mais importante ele tem clareza no desenvolvimento das equaçoes…
56. wilson brant&hellip | abril 11th, 2008 at 10:22:55
Parabens pelo site! Sou pai de um jovem de 15 anos, meu negocio eh entender bem a materia dele para depois tentar somar com ele. Abracos, voltarei mais vezes!
57. naiane&hellip | abril 12th, 2008 at 18:35:48
eu gostei muito desse saite mas bem, voces podia muito por uma colculadora automatica pq nós presisamos e adorariamos muito obrigada por me ouvir mas nao esqueça uma calculadora é muito bom é facil de aprende e é o que preocuro e oq presisamos valeu ai atenda meu pedido to esperendo voltar aqui e o meu pedido realizado se presisar to aqui. meu nome é naiane de oliveira martins tenho14 anos tou na oitava série sou solteira e moro na rua matheus lemes 496 cambé parána brasil fone3251 21 42.
eu nao vou poder ficar mais pq nao achei oque quero a achar calculadora automatica mas vou volta e tenho esperança que vou achar. bjssssssssssssssss xauuuuu valeu aiiii
58. diane vieira&hellip | abril 17th, 2008 at 10:05:59
ótimo.esse site é tudo de bom adorei…
conseguir o q eu queria.
bjos a todos,,,
tchau.
59. Indiara Casanova&hellip | abril 23rd, 2008 at 23:56:27
Me ajudem a resolver: 4 + 2V3 sobre V6-V3+V2-1 (V=raiz quadrada)
60. dionisio papel&hellip | abril 25th, 2008 at 09:38:00
mais conteudo sobre matematica
61. gui&hellip | maio 5th, 2008 at 00:21:26
aFfêÊ..fala sééério..
é o pior site do mundo..
eu já não estava entendendo..depois de entrar aqui então..P-I-O-R-O-U..
62. Angelica&hellip | maio 20th, 2008 at 14:15:30
alguem me explica essas contas…pq amanha tenho prova!
tipo me mandem contas por sits tals….pq nao entendo matematica….é mt dificil é umas das piores materias…mil vezes ingles….por favor algume me ajuda!
Obrigadooooo!
63. José Elias&hellip | maio 23rd, 2008 at 00:50:59
Minha dúvida no desenvolvimento:
(1/3+√8)-(1/3-√8)
64. thiago neto&hellip | maio 27th, 2008 at 21:52:14
gostei esclareceu muito as minhas duvidas
mas deveriam explicar mais
65. rosangela&hellip | junho 1st, 2008 at 19:55:35
Está muito boa a explicação! Sou professora de matemática e consegui tirar uma dúvida para encrementar a minha aula.
muito obrigada.
66. dolfo&hellip | junho 2nd, 2008 at 09:25:35
ei cara!!!!
teu site é muito legal…
mas….
vc num pode deixar quase todas as contas subentendidas não!!!
pq tem gente que procura raionalizações mais detalhadas pra entender melhor!
67. layza&hellip | junho 6th, 2008 at 20:17:50
adorie muito
68. Amayra Cris&hellip | junho 7th, 2008 at 18:24:45
Oi gostaria que alguém me ajudasse a resolver esse exercício:
________1_________
1+raiz de 2+raiz de 3
Estou no aguardo!
Obrigada
69. Ludmylla Larrana&hellip | junho 8th, 2008 at 13:36:24
Parabéns pelo site!
É ótimo me ajudou bastante!
70. Érica&hellip | junho 9th, 2008 at 17:51:44
Urgente!!!!!!!!!!!!!!
Já pesquisei em váaaaaaaaaaarios sites, livros e todo o mais e não consigo encontrar uma explicação para esse sistema linear de 3 equações com 3 incógnitas.
9a-3b+c=0
a+b+c=32
25a+5b+c=0
Gostaria de saber se alguém pode me mostrar a resolução ou simplesmenter me explicar do que se trata.
Muito grata desde já.
71. Isabela Fernanda Dias Ass&hellip | junho 12th, 2008 at 19:06:50
Oi…………eu me chamo isabela e eu queria informar-lhe de que a linguagem usada aki neste site dificulta muito o entendimento.Voçê deveria escrever o passo a passo das contas….pois fui tentar aprender á racionalizar e acabei nao entendendo nada do site.Tente pesquisar todas as regras e o passo á passo das continhas ok?
72. renata.rodrgues terra&hellip | junho 16th, 2008 at 19:07:07
nao gostei!!!!!!!!!!!!!!!
73. Jéssica&hellip | junho 22nd, 2008 at 20:26:44
Como eu multiplico racionais ?
74. JULY&hellip | julho 1st, 2008 at 18:03:55
ÓTIMO MATERIAL!!!CONTUDO, NO TÓPICO DE PRODUTOS NOTÁVEIS FOI DEMOSNTRADA CORRETAMENTE A FÓRMULA DO “QUADRADO DA SOMA”, NO ENTANTO ELA FOI CONSIDERADA IGUAL A “SOMA DOS QUADRADOS”, QUE NESSE CASO É MUITO PARECIDO NA FORMA DE PRONUNCIAR O TERMO, MAS NÃO NO RESULTADO !!!O MESMO ACONTECE COM O CUBO DA SOMA E O QUADRADO DA DIFERENÇA!!!
75. graziele&hellip | julho 3rd, 2008 at 11:03:35
oi.nossa adorei tudo q eu preciso pra estuar prab provas
76. amanda&hellip | julho 21st, 2008 at 10:46:11
eu adorei o o seu site é muito bom saber que existe varios recursos para nos ajudar!!
eu amei continuem assim!
bjssssssssss
77. gustavo&hellip | julho 29th, 2008 at 19:05:13
eu gostei muito desse site é muito maneiro !!! agora eu sei mais sobre matematica de 8 serie e muito divertido aprende !!valeu!!!
78. Andressa&hellip | agosto 5th, 2008 at 14:55:15
Gostei,mais ai nao tem produtos notaveis contas e respostas que eu to fazendo um trabalho akii.beijos…
79. tandara santiago&hellip | agosto 5th, 2008 at 17:46:27
gostaria q vc me explicasem como se resolve o 1,2eo 3 caso da racionalização obrigada”!!
80. jandeilson&hellip | agosto 22nd, 2008 at 13:26:44
entendi dessa vez a prof qui eu estudo naum ensina nada qui preste agora posso fazer uma prva traquilo com essa esplicação ei isso foi uma desabafo valeu bjus
81. Lenon Matos&hellip | agosto 24th, 2008 at 15:23:58
Muito bom esse documentário de voces ira me ajudar muito em provas de vesttibular vlw
82. Lucas&hellip | agosto 28th, 2008 at 14:03:24
Sem dúvida nenhuma uma das melhores explicações q já tive, tirei todas as minhas dúvidas, obrigado.
83. Taís&hellip | setembro 10th, 2008 at 22:48:03
mas por que racionalizamos o denominador?
obrigada
84. bruna&hellip | setembro 16th, 2008 at 02:00:32
muito bom essa explicação…me ajudou muito!
obrigada
85. henrique&hellip | setembro 16th, 2008 at 22:55:02
FALA SERIO MEU, QUEM TIROU TODAS AS DULVIDAS NESSA EXPLICAÇAO
(E POR QUE NAO TINHA NEM UMA DULVIDA)
SIMPLESMENTE JA SABIA
(FOI GREGO PRA MIN)
86. Pedro Meneses&hellip | outubro 10th, 2008 at 11:10:09
Obrigado Uma Das Melhores Explicações q ja tive Very Thankyou
87. Ânnela&hellip | outubro 16th, 2008 at 10:13:04
respondendo a Taís …
é por que nenhum denominados pode ficar com raís…
beijoos!!!
88. rafaela edna barbosa da s&hellip | outubro 17th, 2008 at 23:35:40
Me ajudou muito mesmo até passei na prova do colégio militar
Obrigada!!
89. katarine pereira da silva&hellip | outubro 26th, 2008 at 18:34:22
nossa gostei muuuuuuuuuuuuuuuuuuuuuuuuiito desse site e d+
bjokas♥ kaathy♥
90. alessandra&hellip | novembro 10th, 2008 at 18:42:37
não achei nadaqueme enterce!!!!!!!!!!!!!!!!!!!
thauuuuuuuuuuuuuuuuuuuuuuu!
91. quintino&hellip | dezembro 15th, 2008 at 09:17:54
valeu és barra
92. Osvaldo R Moura&hellip | fevereiro 1st, 2009 at 11:34:04
Gostei muito da matéria pelos exemplos desenvolvidos, são muito úteis.
93. jonathan dos santos viana&hellip | fevereiro 6th, 2009 at 12:26:26
gostei muito dessa aula on line e pretendo visita-lo cada vez mais e mais
94. Thyago Câmara Costa&hellip | fevereiro 8th, 2009 at 16:33:36
gostei muito desse site! respondeu muitas das minhas perguntas sobre racionalização.
obrigado.
95. iago&hellip | março 14th, 2009 at 16:13:28
muito lekal ;) …
96. Kíssila&hellip | março 16th, 2009 at 14:24:19
Parabéns pelo site..
Me exclareceu bastante..
97. ires&hellip | março 17th, 2009 at 17:31:22
obrigada, tirei muitas duvidas.
98. jeronimo&hellip | março 17th, 2009 at 19:08:28
muito complicado
99. gabis,&hellip | março 28th, 2009 at 17:06:54
MUIIITO³ show parabéns!
100. pedro da silva&hellip | março 29th, 2009 at 14:07:01
n gostei n explicabem
101. bianca m dantas&hellip | abril 3rd, 2009 at 16:53:32
ta faltando muita coisa aqui divia ter modelos de contas montadas
nao gostei porque so tem explicaçoes mais nao tem modelos
102. André Barcelos&hellip | abril 15th, 2009 at 16:21:26
Muito elucidativo os exercícios resolvidos, gostaria de parabenizar esse exelente trabalho.
103. karol&hellip | maio 6th, 2009 at 23:19:09
adoraria se vooc`s colocassem exercicios no site pra nós alunos resolvermos!!
seria interessante …e vim avisar que pela primeira vez em doiz anos nao fiquei de recuperaçao em matematica no primeiro bimestre!ufa …tanto tempo estudando ate que consegui!!
bjao
104. Denilson&hellip | maio 17th, 2009 at 22:20:59
não houve explicação clara em relação a minha pesquisa.
105. Elvis Da Costa&hellip | maio 30th, 2009 at 04:37:07
Gostaria De Entender Um Pouco Mais Sobre Equações, De Primeiro é 2º Grau Obrigado.
106. gordana&hellip | maio 30th, 2009 at 19:09:25
aff…
num gustei naum!!!!
na proxima vez ve se melhora…
107. Robison&hellip | junho 14th, 2009 at 11:36:09
Muito bom. Me bastante na construção de provas sobre o assunto
108. elvis&hellip | junho 23rd, 2009 at 21:25:56
nao entendi nada nao explica nada nao gostei ve se melhora depois plz
109. alex&hellip | julho 5th, 2009 at 22:38:54
estou em duvida na seguinte questao: 4√243
110. Ana Júlia&hellip | julho 13th, 2009 at 16:18:30
Não entendi nada
111. ^^JANA^^&hellip | setembro 3rd, 2009 at 10:34:49
PODERIA TER MAIS QSTOES E EXPLICAR BEM MELHOR!!OK??
112. Jorgete&hellip | setembro 28th, 2009 at 21:31:19
Muito obrigado, me ajudou bastante. A minha memória às vezes falha quando o assunto é matemática básica.
113. sonia&hellip | outubro 11th, 2009 at 14:50:05
gostei muito mais como eu perde as esplicações do meu professor eu não consigo entender tem como voce me ajudar
114. othon marliere&hellip | janeiro 14th, 2010 at 21:02:11
muito obrigado pelo conteudo, parabens
115. Marcela&hellip | março 4th, 2010 at 17:29:19
Muito obrigada pela sua ajuda!!
116. Armindo Ngola&hellip | março 9th, 2010 at 05:16:56
muito obrigado por nos ter proporcionado estes exercicios resolvidos e explicados me ajudou bastante. thank you.
117. ANA LAURA&hellip | abril 5th, 2010 at 19:17:54
MUTO FACIL
118. loiane&hellip | abril 6th, 2010 at 14:16:45
nao entendi nada…vcs poderiam ser mais claros…muito dificil…
obrigado *
119. Murilo&hellip | abril 15th, 2010 at 20:52:31
Muito facil!
120. kauana&hellip | maio 17th, 2010 at 20:59:03
vooçs podiam ser mas claros obg ;D
121. Lourdes oliveira&hellip | junho 1st, 2010 at 07:32:20
Estava com dificuldade em entender que precisamos usar a
fatoração para resolver alguns casos. Como este assunto foi
dado na série anterior, só temos que relembrar e, então, tudo
acontece. Muito grata pela ajuda.
122. eliane&hellip | agosto 21st, 2010 at 07:43:33
gostaria de ex: mais completo tipo passo a passo
1º subtrai multiplica e soma?
Deixe seu Comentário
São permitidas as seguintes tags:
<a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <strike> <strong>
Trackback this post | Subscribe to the comments via RSS Feed