René Descartes (31 de Março de 1596, La Haye en Touraine, França — 11 de Fevereiro de 1650, Estocolmo, Suécia), também conhecido como Cartesius, foi um filósofo, um físico e matemático francês. Notabilizou-se sobretudo pelo seu trabalho revolucionário da Filosofia, tendo também sido famoso por ser o inventor do sistema de coordenadas cartesiano, 1637, que influenciou o desenvolvimento do Cálculo moderno. Note que com essa invenção Descartes mostrou como traduzir problemas de geometria para a álgebra.

Visite a Wikipédia, de onde o trecho acima foi extraído, para saber mais sobre René Descartes.

Em linhas gerais, um sistema de coordenadas cartesiano consiste de um esquema que permite especificar pontos em um determinado espaço com n dimensões. Assim, por exemplo, a reta corresponde à dimensão 1 (n = 1), o plano à dimensão 2 e o espaço à dimensão 3.

Um ponto qualquer em uma reta orientada ou eixo orientado x, com origem O, o centro das coordenadas e que corresponde ao valor 0 (zero), é representado por um número real. Se positivo estará localizado à direita e se negativo à esquerda de O. Para o assunto a ser tratado é necessário começar pela definição a seguir.

Plano Cartesiano

O plano cartesiano é definido por dois eixos orientados x e y – as dimensões -, perpendiculares entre si, que se cruzam no ponto O, origem de ambos os eixos, conforme figura a seguir.

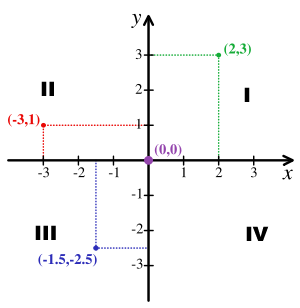
Observações:

• O eixo x é denominado de eixo das abcissas ou eixo Ox;
• O eixo y é denominado de eixo das ordenadas ou eixo Oy;
• Os dois eixos dividem o plano em quatro quadrantes (I, II, III e IV na figura);
• Cada ponto P do plano cartesiano é identificado por dois números reais x e y e é representado na forma de um par ordenado (x,y), também chamado de coordenadas do ponto P, onde x é a abcissa e y a ordenada;
• Um ponto P é obtido por meio do encontro das perpendiculares aos eixos Ox e Oy traçadas a partir de sua abcissa e de sua ordenada. Veja na figura a representação do ponto P = (2,3);
• A origem O é representada pelo par ordenado (0,0);
• Os pontos do quadrante I são representados pelos pares ordenados (x,y) em que x e y são positivos;
• E os do quadrante II pelos pares ordenados (x,y) em que x < 0 e y > 0;
• Os do quadrante III pelos pares ordenados (x,y) em que x e y são negativos;
• Os pontos do quadrante IV são representados pelos pares ordenados (x,y) em que x > 0 e y < 0;
• Um par ordenado (a,b) é igual a outro par ordenado (c,d) se, e somente se, a = c e b = d;
• Em um par ordenado (a,b), se a é diferente de b, então (a,b) é diferente do par ordenado (b,a). Determine, por exemplo, no plano cartesiano os pontos P = (1,2) e Q = (2,1) para comprovar a afirmação;
• De forma resumida, podemos afirmar que, no plano cartesiano, cada ponto é representado por um único par ordenado (a,b), a e b números reais. A recíproca também é verdadeira, ou seja, cada par ordenado (a,b) representa um único ponto no plano cartesiano;
• E, por fim, o plano cartesiano é obtido associando-se a cada um dos eixos o conjunto dos números reais.

Produto Cartesiano

Sejam A e B dois conjuntos não vazios. Definimos como produto cartesiano de A por B o conjunto A x B cujos elementos são todos os pares ordenados (a,b) em que a pertence a A e b pertence a B:

A x B = {(a,b) | a Ɛ A e b Ɛ B}

Observações:

• O símbolo A x B lê-se “A cartesiano B” ou “produto cartesiano de A por B”;
• Se o conjunto A é diferente do conjunto B, A e B diferentes do conjunto vazio, então A x B é diferente de B x A, veja exemplo abaixo;
• A x ø = ø, ø x A = ø e ø x ø = ø;
• Se A ou B é infinito e nenhum deles for vazio, então A x B é infinito;
• A x A pode ser também representado por A², que se lê “A dois”;
• Se A e B são finitos e A tem m elementos e B tem n elementos, então A x B tem m.n elementos: n(A x B) = n(A).n(B) = m.n.

Exemplo extraído do livro Fundamentos de Matemática Elementar, Vol 01, Conjuntos e Funções – ver referências no final do post:

Se A = {1,2,3} e B = {1,2} então:

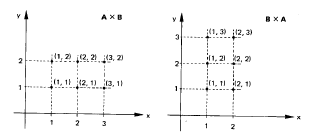
A x B = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)}

e

B x A = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)}

cujas representações no plano cartesiano são as seguintes:

Relação Binária

Dados dois conjunto A e B não vazios, chama-se relação R, ou mais simplesmente relação binária, de A em B a qualquer subconjunto de A x B. Uma relação R de A em B é representada pelo símbolo R: A -> B:

R: A -> B <=> R C A x B

Exemplo:

Se A = {1,5} e B = {3,4,6}, então A x B = {(1,3), (1,4), (1,6), (5,3), (5,4), (5,6)}. Logo:

R = {(1,3), (1,6), (5,4)}

S = {(5.4)}

T = {(1,3), (1,4), (5,3), (5,6)}

são relações de A em B, uma vez que R, S e T são subconjuntos de A x B.

As relações que estabelecem uma condição matemática para que um determinado par ordenado (x,y) pertença à uma relação são de grande importância. Vejamos alguns exemplos para ilustrar o fato.

Se A = {1,3,4} e B = {2,4}, então A x B = {(1,2), (1,4), (3,2), (3,4), (4,2), (4,4)}. São relações de A em B:

a) R = {(x,y) Ɛ A x B | x = y} = {(4,4)}

b) S = {(x,y) Ɛ A x B | x/y Ɛ Z} = {(4,2), (4,4)}

c) T = {(x,y) Ɛ A x B | y – x = 1} = {(1,2), (3,4)}

Domínio e Imagem

Seja R uma relação de A em B.

1. Chama-se domínio de R, e denotamos por D(R), o conjunto de todos os primeiros elementos dos pares ordenados pertencentes a R. Ou, alternativamente, o conjunto de todos os elementos de A que estão associados a pelo menos um elemento de B.

2. Chama-se imagem de R, e denotamos por Im(R), o conjunto de todos os segundos elementos dos pares ordenados pertencentes a R.

Com base no exemplo anterior, temos:

a) D(R) = {4} e Im(R) = {4}

b) D(S) = {4} e Im(S) = {2,4}

c) D(T) = {1,3} e Im(T) = {2,4}

Referências

1. Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977;
2. Matemática para o Ensino Médio: Volume Único, Manoel Jairo Bezerra, São Paulo, Editora Scipione, 2001.