Exercícios resolvidos sobre Radiciação com o objetivo de fixar os conceitos e as propriedades já tratadas no artigo de mesmo nome. Inicia com a questão do leitor identificado como HENRIQUE (comentário #33) sobre raiz de índice m da raiz de índice n ou como dito por ele, radical duplo.
Em seguida, serão resolvidos outros exercícios em que procuro cobrir todas as propriedades esboçadas no texto teórico acima mencionado. Em caso de dúvidas leia o artigo cujas propriedades serão aqui apenas assinaladas por P1, P2, …, P7 quando usadas.
Exercício 1: A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a:
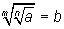
O que a propriedade diz? Diz que o resultado é o mesmo se você calcula a raiz de índice n de a e depois a raiz de índice m do valor obtido dessa operação ou se você calcula, diretamente, a raiz de índice mn de a. Faça esses cálculos com a raiz cúbica da raiz quadrada de 64 e a raíz sexta de 64, e veja que o resultado obtido é igual a 2 em ambos os casos.
Solução 1:
Primeiro, lembro a seguinte propriedade de potenciação: em uma igualdade ao se elevar ambos os seus membros à uma potência de grau m ela não se altera. Desse fato e supondo que:
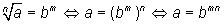
vem (elevando ambos os membros à potência m) que:
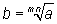
e pela definição de radiciação:
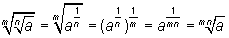
o que conclui a demonstração.
Solução 2:
Uma outra maneira de demonstrar a propriedade (P5) é através da aplicação da propriedade P7:
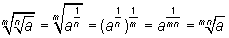
Exercício 2: Calcular
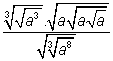
Solução:
Para facilitar a explicação, e consequentemente o entendimento, vamos, inicialmente, tratar separadamente cada membro da expressão, onde se indicam as propriedades utilizadas em cada passagem:
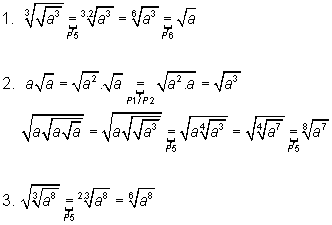
Assim de 1, 2 e 3 obtemos:
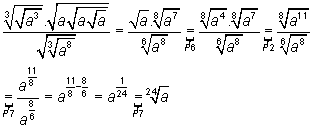
Exercício 3: (UFCE) Simplificar a expressão:
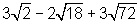
Solução:
Exercício simples que se baseia na decomposição em fatores primos de cada radicando e da utilização da propriedade P1, como você pode observar no detalhamento a seguir. Tenha em conta que na soma ou subtração de radicais, cada parcela deve ser considerada isoladamente para se obter o resultado de uma expressão. Ou seja, não se aplica que a soma de duas raízes de mesmo índice é igual a raiz da soma, como é o caso do produto, por exemplo.
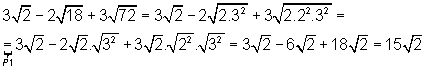
Exercício 4: Calcular o quociente:
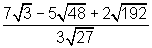
Solução:
Outro exercício de solução simples onde demonstro o uso das propriedades P1 e P3, e novamente, faço uso da decomposição em fatores primos dos radicandos:
Exercício 5: Escrever em ordem de grandeza crescente os radicais:
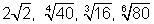
Solução:
Para fazer a comparação entre os radicais devemos, inicialmente, reduzí-los ao mesmo índice. Isto é feito calculando o mínimo múltiplo comum (mmc) dos índices e, após, aplicando a propriedade P6. O mmc(2, 4, 3, 6) = 12 e reescrevendo os radicais (P6) vem:
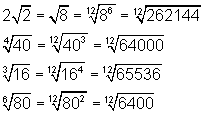
Agora, basta considerar a ordem dos radicandos para estabelecer a ordem crescente dos radicais:
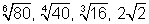
Exercício 6: Efetuar
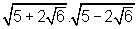
Solução:
Esboçada a seguir, onde utilizamos o fato de que o produto da soma pela diferença de dois números é igual ao quadrado do primeiro menos o quadrado do segundo (produto notável – PN) e as propriedades da Radiciação indicadas:
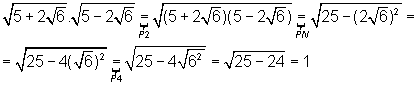




mar 17, 2012 @ 12:26:44
Eu sou 8 serie e ja sei desse conteudo todo.Tenho uma prova para amanha,e ja vou tira de letra esse sate e bacana deu pra levanta o animo!
mar 06, 2012 @ 19:01:11
ñ entendi nada eu tenho lição para fazer para amanha se eu ñ fizer vou trazer um papel para minha mãe assinar que eu ñ fiz lição e minha mare vai me matar
out 14, 2011 @ 21:23:02
não me ajudou em nada ! eu quero mais explicação , tenho prova amanhã e preciso saber esse assunto , mas tudo bem ! eu irei procurar em outro site . beijoos !
jun 30, 2011 @ 21:39:57
a matematica estaa na nossas vidas
jun 26, 2011 @ 19:25:43
adorei tenho prova amanha e entendi tudo, mas queria mais exercícíos
jun 16, 2011 @ 15:49:56
matematica e bom de mais.
jun 15, 2011 @ 19:56:15
eu gostei muito dessas explicasoes eu queria dessen mais
maio 25, 2011 @ 10:12:35
eu gostaria de saber sobre como eu poderia resolver um exercico de propriedades i depois decompor os radicaias mas nada encontrado!
maio 12, 2011 @ 08:06:59
é mto ruim !!!!
jul 16, 2011 @ 13:30:33
alem de ruim faltou radiciaçao com bases diferentes
fev 07, 2012 @ 14:18:14
isso mesmo
abr 18, 2011 @ 20:49:56
Eeeu não entendii muitoo nãoo maiis ta boom ..
Eeeu Amoo MATEMÁTICA ♥
abr 13, 2011 @ 14:19:25
MATEMÁTICA A MELHOR MATÉRIA DO MUNDO!!!!
abr 07, 2011 @ 14:41:16
quero que resolvam pra mim um de simplificação de 3letras e 3numeros por favor
abr 06, 2011 @ 15:21:20
odeio matematica ñ suporto so estudo pq tenho q estudar
abr 08, 2011 @ 07:07:57
eu até gostava de amtematica mas com meu prof novo n tow começando a odeiar aff
abr 13, 2011 @ 14:20:27
nao fala assim nao é muito massa
dez 27, 2011 @ 20:42:18
Vdade, se vc não gosta, vai dar uma lida, Interpretar virgula em direito. ‘-‘
mar 28, 2011 @ 17:09:55
odeio matematica para que que eu vou usar isso na minha vida
?
mar 31, 2011 @ 17:18:24
Pra nada querida =) a não ser que você queria ter um futuro pelo menos confortável, passando em testes como o ENEM, vestibulares ou concursos.
abr 11, 2011 @ 20:45:46
matematica so presta para professor porque eu nao entendo
abr 11, 2011 @ 20:40:56
para voce ser alguem na vida
emtendeu
abr 13, 2011 @ 14:21:27
para onde vc for vc vai usar a matematicaa
abr 18, 2011 @ 17:02:12
Utilização da matemática:
Para patrão: como auferir lucros
Para empregados: como conferir holerit
mar 10, 2012 @ 11:13:27
A matematica e uma disciplina muito fixe so nao entende quem nao quer
fev 13, 2011 @ 16:25:39
gostei muito, mas deveria ter mais exempos.
fev 09, 2011 @ 10:47:56
gabiii a resposta é 19 raiz de 5 me add msn lolo_xuaua@hotmail.com,q eu passo a conta completa pra vc! :D
fev 08, 2011 @ 14:50:02
eu naun estou conseguindo entende muito esse assunto sobre radiaçao
minha professora repassou 22 exercicios sobre isso mas naun estou conseguindo resolve nenhun poderian me ajudar a entender mais o assunto …ex esse :
2 raiz 45 + 3 raiz 125 – 6 raiz 20 + 3 raiz 80 – 2 raiz 5 ( o resultado e 19 raiz 5 )???
raiz de 6 sobre raiz de 2 ???
obrigadoo
dez 07, 2010 @ 20:49:32
legal eu gostei muito bom
jul 22, 2010 @ 16:26:34
Excelente!
Eu adorei sua forma direta e precisa de passar os conteúdos. :D
Eu aprendi bastante aqui, mas o mais importande, abriu a janela para que eu
aplique esse conteúdo com mais certeza.
Obrigado. Mesmo.
ótimo site, diga se de passagem…
jul 08, 2010 @ 21:18:21
Vcs poderiam por favor me ajudar a desenvolver e solucionar essa soma?
raiz quadrada de 3 + raiz quadrada de 27 a resposta eh 4raiz qaudrada de 3, mas eu nao acertei como chegar a esse valor
abr 18, 2011 @ 17:07:09
raiz de 27 é equivalente a raiz quadrada de (3 elevado a 2) vezes (3), então fica 3 raiz de 3 mais 1 raiz de 3 que são 4 raiz de 3.
Experimente escrever na notação matemática, fica mais fácil de entender.
Luz e paz
abr 25, 2011 @ 18:35:41
Fácil, Nana. Fatora o 27, ai fica 3 elevado a 3=( 3³). Então fica raiz quadrada d 3 + raiz quadrada de 3³, agora vc desmembra o 3³ = 3².3¹. Retira o 3² do radical fica 3 raiz quadrada de 3. Agora é só somar os radicais, raiz de 3 + 3 raiz de 3. = 4 raiz de 3. Ok? Meio embaralhado por falta de icones. Espero ter ajudado. Bjs.
jul 05, 2010 @ 10:49:54
bom dia amiguinho eu gostaria de saber essas continhas se não minha mamãe não dexa eu ir pra catequese por favor me ajude lol
jun 21, 2010 @ 20:38:00
Maravilhoso assim eu ate passo de serie ^^^^^^
maio 27, 2010 @ 14:49:56
Gostei bastante, mas tem poucos exercícios.
maio 01, 2010 @ 15:28:09
parabens pelos otimos exercicios.
será que dava para repetir o exercicio 4 com todas as passagens, aquela depois do antepenultimo igual eu nao entendi e nao achei na net
obrigado
azevedo25@hotmail.com
abr 28, 2010 @ 16:19:10
Brigado, mt boom o site.
Será que vc poderia coolocaar outroso exemplos com quocientes com 2 ou 3 raízes ?
;*
abr 27, 2010 @ 15:33:01
pra ser sincera eu ñ gostei porque eu ñ entendi absolutamente nadica de nada
abr 12, 2010 @ 19:31:15
não gostei, não entendi nada u_u
abr 11, 2010 @ 21:58:03
obrigado naum era exatamente o q eu queria mais me ajudou
abr 08, 2010 @ 08:41:42
ainda bem… que eu não precisei calcular / hihi!!
abr 05, 2010 @ 21:40:38
Muito obrigado me ajudou muitoo !
abr 04, 2010 @ 11:20:06
qual a raiz de 1.296/1.849/4096/2,25
mar 29, 2010 @ 22:55:03
Obrigado, vc me ajudou muito! Gostei muitoo ! As vezes tenho muito dificuldade em Matemática ¬¬’ , e esse site me ajuda sempre! Tenho muitas duvidas sempre..Abraçoos :)
mar 29, 2010 @ 17:32:41
num tem nada aqui
mar 25, 2010 @ 17:32:03
ihhh tem pouco exercicio e todos são faceis
mar 18, 2010 @ 13:10:28
GOSTEI
mar 18, 2010 @ 09:19:56
isso irá sert muito importante no relatório que o professor nos deu para fazer ! ‘
mar 15, 2010 @ 10:13:55
Veý tou mi passando mas estudando mas uns poucos chego la (h)
mar 14, 2010 @ 22:31:22
é muito dificil eu ñ sei de nada e to na oitava serie.
mar 12, 2010 @ 08:31:47
quero aprender bem a matematica…
mar 04, 2010 @ 22:30:39
poxa velho , ñ entende merda nenhuma , mas de qualquer forma . vlw!!
dez 17, 2009 @ 17:04:16
gostaria de saber sobre a evolução da simplificação sabendo que a matemática é ciência muito linda
dez 12, 2009 @ 00:02:33
Gostaria que resolvesse a seguinte atividade detalhadamente: Em um triangulo retangulo OAB, retangulo em O, com OA = a e OB = b são dados os pontos P em OA e Q em OB de tal maneira que AP=PQ=QB=x. Calcular o valor de x.
Obrigada!!!
dez 11, 2009 @ 11:35:17
por favor sera que vc podia explica sobri potencia produtos nootaveis e radiciaçao nao e como ta ai os calculos sao menires para eu estuda para prova segunda que vem
dez 03, 2009 @ 18:28:15
muito obrigado mesmo me ajudou d++++++++!!
nov 25, 2009 @ 10:26:01
Resolve para mim!
Na 7º série B estão matriculados 14 meninos e 19 meninas. Um desses alunos será sorteado pela professora de geografia, para apresentar um seminário. Qual é a probabilidade, em porcentagem, de uma menina ser sorteada para essa apresentação?
nov 20, 2009 @ 12:52:17
,o Sr. descreveu:
Exec1: A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a. O mn então é a multiplicação?
set 07, 2009 @ 14:41:02
Prof. por favor me esclareça uma dúvida, o Sr. descreveu:
Exercício 1: A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a. O mn, nesse caso é uma multiplicação?
acessei a página –
http://www.nghorta.com/2006/07/29/exercicios-resolvidos-3-radiciacao/comment-page-4/
Agradeço
ago 29, 2009 @ 20:35:11
Gostaria que vcs me mandassem a história, como surgiu e de onde sugiu a radiciação, preciso para trabalho da falcu
l,dade o mais rapido possível. Obrigado
ago 11, 2009 @ 21:38:41
E simplificação de radicais?
abr 13, 2011 @ 14:24:12
o que vc quer saber sobre isso?
jul 24, 2009 @ 13:43:13
radiciaçao matematica muito importante para aprova e para ha vida.