fev
Conjuntos Numéricos
Publicado por
A história nos mostra que desde muito tempo o homem sempre teve a preocupação em contar objetos e ter registros numéricos. Seja através de pedras, ossos, desenhos, dos dedos ou outra forma qualquer, em que procurava abstrair a natureza por meio de processos de determinação de quantidades.
E essa procura pela abstração da natureza foi fundamental para a evolução, não só, mas também, dos conjuntos numéricos. E é sobre eles que passamos a dissertar.
Conjunto dos Números Naturais
Como decorrência da necessidade de contar objetos surgiram os números naturais que é simbolizado pela letra N e é formado pelos números 0, 1, 2, 3, …, ou seja:
N = {0; 1; 2; 3; …}
Um subconjunto de N muito usado é o conjunto dos números naturais menos o zero, ou seja N – {0} = conjuntos dos números naturais positivos, que é representado por N*.
Observações:
- Em N são definidas apenas as operações de adição e multiplicação;
- Isto é fato pois se a e b são dois números naturais então a + b e a.b são também números naturais. Esta propriedade é conhecida como fechamento da operação;
- Valem as propriedades associativa, comutativa e elemento neutro (0 para a adição e 1 para a multiplicação) para as duas operações e a distributiva para a multiplicação em N. Veja o artigo Produtos Notáveis para maiores detalhes sobre essas propriedades, no caso da multiplicação, onde o conjunto universo considerado é o dos números reais, que abordaremos mais abaixo, e que são válidas para N;
- Em N a subtração não é considerada uma operação, pois se a diferente de zero pertence a N o simétrico -a não existe em N.
Como consequência, surge um novo conjunto para atender essa necessidade.
Conjunto dos Números Inteiros
Chama-se o conjunto dos números inteiros, representado pela letra Z, o seguinte conjunto:
Z = {…, -3; -2; -1; 0; 1; 2; 3; …}
No conjunto Z distinguimos alguns subconjuntos notáveis que possuem notação própria para representá-los:
- Conjunto dos inteiros não negativos: Z+ = {0; 1; 2; 3; …};
- Conjunto dos inteiros não positivos: Z- = {…; -3; -2; -1; 0};
- Conjunto dos inteiros não nulos: Z* = {…, -3; -2; -1; 1; 2; 3; …};
- Conjunto dos inteiros positivos Z+* = {1; 2; 3; …};
- Conjunto dos inteiros negativos Z-* = {…; -3; -2; -1}.
Note que Z+ = N e, por essa razão, N é um subconjunto de Z.
Observações:
- No conjunto Z, além das operações e suas propriedades mencionadas para N, vale a propriedade simétrico ou oposto para a adição. Isto é: para todo a em Z, existe -a em Z, de tal forma que a + (-a) = 0;
- Devido a este fato podemos definir a operação de subtração em Z: a – b = a + (-b) para todo a e b pertencente a Z;
- Note que a noção de inverso não existe em Z. Em outras palavras, dado q pertencente a Z, diferente de 1 e de -1, 1/q não existe em Z;
- Por esta razão não podemos definir divisão no conjunto dos números inteiros;
- Outro conceito importante que podemos extrair do conjunto Z é o de divisor. Isto é, o inteiro a é divisor do inteiro b – simbolizado por b | a – se existe um inteiro c tal que b = ca;
- Os números inteiros podem ser representados por pontos de uma reta orientada ou eixo, onde temos um ponto de origem, o zero, e à sua esquerda associam-se ordenadamente os inteiros negativos e à sua direita os inteiros positivos, separados por intervalos de mesmo comprimento;
- Cada ponto da reta orientada é denominado de abcissa;
- Em Z podemos introduzir o conceito de módulo ou valor absoluto: |x| = x se x >= 0 e |x| = -x se x < 0, para todo x pertencente a Z. Como decorrência da definição temos que |x| >= 0 para qualquer número inteiro.
Conjunto dos Números Racionais
O conjunto dos números racionais, simbolizado pela letra Q, é o conjunto dos números que podem ser escritos na forma de uma fração p/q, com p e q inteiros quaisquer e q diferente de zero:
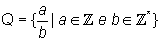
Como todo número inteiro pode ser escrito na forma p/1, então Z é um subconjunto de Q. Valem também para o conjuntos dos números racionais as notações Q* (conjunto dos números racionais não nulos), Q+ (conjunto dos números racionais não negativos) e Q- (conjunto dos números racionais não positivos).
Observações:
- São válidas todas as propriedades vistas para o conjunto dos números inteiros;
- Além disso é válida a propriedade simétrico ou inverso para a multiplicação. Isto é, para todo a/b pertencente a Q, a/b diferente de zero, existe b/a em Q tal que (a/b)(b/a) = 1;
- Decorre da propriedade acima que é possível definir a operação de divisão em Q* da seguinte forma (a/b):(c/d) = (a/b).(d/c), para quaisquer a, b, c e d pertencente a Q;
- Todo número racional p/q pode ser escrito como um número decimal exato (ex: 1/2 = 0,5) ou como uma dízima periódica (1/3 = 0,333…).
Números Irracionais
Como o próprio nome sugere um número irracional é todo número não racional, isto é, todo número que não pode ser escrito na forma de uma fração p/q, onde p e q são inteiros e q diferente de zero.
São exemplos de números irracionais a raiz quadrada de 2 e a raiz cúbica de 3, ou seja, nenhum deles pertence a Q.
A título de ilustração vamos demonstrar, pela teoria do absurdo, que a raiz quadrada de 2 não pertence a Q.
Suponhamos que raiz quadrada de 2 é racional e admitamos que possa ser escrita como uma fração irredutível a/b, b diferente de zero:
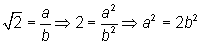
Da expressão acima concluímos que a ao quadrado é par e que, portanto, a é par. Logo a = 2m, com m inteiro. Substituindo o valor de a na expressão anterior vem que:
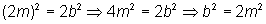
Da mesma forma obtemos que b também é par, o que é um absurdo pois a/b é irredutível, ou seja, a e b são primos entre si, e portanto têm como divisor comum apenas o número 1, isto é, mdc(a,b) = 1.
Caso deseje obter maiores informações sobre as operações com números irracionais consulte os artigos publicados no blog na categoria Matemática.
Conjunto dos Números Reais
O conjunto dos números reais, simbolizado pela letra R, é o formado por todos os números racionais e por todos os números irracionais:
R = {x | x é racional ou x é irracional}
Desse modo todos os conjuntos numéricos (N, Z e Q), bem como o conjunto dos números irracionais são subconjuntos de R.
Da mesma forma destacamos três outros subconjuntos de R: R* = conjunto dos reais não nulos, R+ = conjunto dos reais não negativos e R- = conjunto dos reais não positivos.
Conjunto dos Números Complexos
O conjunto dos números complexos, simbolizado pela letra C, foi criado para dar sentido às raízes de índice par de números negativos, com a definição da unidade imaginária i igual a raiz quadrada de -1, e são constituídos de elementos na forma a + bi, onde a e b são reais. Desse fato temos que R está contido em C.
Referências:
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977;
- Matemática para o Ensino Médio: Volume Único, Manoel Jairo Bezerra, São Paulo, Editora Scipione, 2001.
Posts Relacionados
- Questionarious #2 – Conjuntos
- Curiosidade Matemática #5 – Método de Pitágoras para Calcular a Potência de Grau 2 de um Número
- Conjuntos: Operações – Parte II
- Conjuntos: Noções Básicas – Parte I
- Curiosidade Matemática #4 – Conceitos
- Progressões – Parte I
- Equações Exponenciais
Posts relacionados trazidos a você pelo Yet Another Related Posts Plugin.
Imprima este artigo | Envie este artigo para um(a) amigo(a) | 150.203 views
- Bookmark :
- Digg
- del.icio.us
- Stumbleupon
- Redit it
140 Respostas para “Conjuntos Numéricos”
Brasileirão 2010 – Próximos Jogos
Os horários dos jogos estão em horário local. Por favor clique aqui para converter para seu fuso horário.
Dia: 31/07/2010 Data-Hora Jogos 31/07 18:30 
FLU -:- CAP 
31/07 18:30 
AGO -:- GFC 
31/07 18:30 
SPFC -:- CESC 
Dia: 01/08/2010 Data-Hora Jogos 01/08 16:00 
PAL -:- COR 
01/08 16:00 
ECV -:- BOTA 
01/08 16:00 
AVAÍ -:- GEC 
01/08 16:00 
INTER -:- GRE 
01/08 18:30 
AMG -:- CRZ 
01/08 18:30 
GPRU -:- SFC 
01/08 18:30 
FLA -:- VASCO 
Posts Recentes
Categorias
Tags
Posts View
Plugin bVGallery
World Cup 2010
Feeds
Visitantes
- 12 currently online
- 67 maximum concurrent
- 3188324 total visitors
oieeee galeraaaaa
brigada msm pelo teu blog, site, seja láh oque for….
táh mi ajudandu, amanhã teim prova iiii prisciso mutcho dissu
weeee³
arega.tanks ((obrigada eim japortu.ingrês))
=3
naum liga as palavritas erradas, sabi como é neah, essi troço di “yakut”((orkut))…só insina palavras errand…¬¬’
XD~~
kissus* pla todos((kiss))
…
nr naturais = {0,1,2,3,4…}
nr inteiros = {…-2,-1,0,1,2…}
nr racionais={3,2;0,66…4,4;9/2;…}
O zero pertence aos nrs naturais….( com certeza)
Amigo, sua pagina é ótima. Pena às vezes, como um comentário do (21) que se diz professor e não gostou do seu site. ( o rapaz se diz professor, mas nem sabe escrever, ou seja, sabe escrever com muitos erros ortográficos ( professor ???)
gostaria de receber a demonstração de que a raiz cubica de 3(√3 ) não pertence aos Q(RACIONAIS)..ficaria muito grato em receber..muito aobrigado!!!!!!
Isso me ajudou muito gostei muito isso foi bem rezumido
e me ajudou na materia.
tem que explicar, mais a parte de numeros reais
é um bom site
adorei vei mais tem q por mais contas
gostei, mais poderia ter mais exemplos ,como exercícios feitos e exemplificar os 5 tipos de operaçoes. porém fica muito complicado
eu notei uma pequena falha ,falta mais exemplos com numeros naturais .Mais a não ser por isso ,gostei muito e aprendi um pouco mais com esse estudo.
gostei do blog ,mas , gostaria q junto dos exemplos tivesse exercicios.por favor façam exercicios ,eles nos ajudam a fixar mais rápido .obrigada .boa noite!!!!!!!1
preciso ensinar à minha filha à fazer expressâo, numèricasrepresentacâo de simbolo,numeros naturais,inteiros,racionais,símetrico de cada numero,e nâo sei fazer esses calculos para segunda -feira me ajudem pelo amor de deus.
esse site é otimo ta me ajudando muito
principalmente agora pra prova do CEFET
parabens pra vc….site de catiguria….
oq é conjunto finito me ajudem eu to penanado pra acha isso e ñ estou achando nada q me esplique d uma maneira geral
eu achei tudo isso uma chatisse melhora esse site
Gostei do site, mais quero receber via e-mail, o mais rápido possível Dez questões dos conjuntos numéricos espero ansiosa
obrigada
beijos***
achei muito legal tudo
Bando de retardados
é claro que o 0 tá incluido no conjunto dos numeros naturais(N)
dããrr
vcs tão errados
Burros
resolvam esta: Um estudante em férias observou que durante d dias:
* choveu 7 vezes, de manhã ou de tarde;
*houve 5 manhãs sem chuvas;
*houve 6 tardes sem chuvas;
Calcule d?
gostei muito desse site e muito interessante..
Não entendí o questionamento de Maria em relação ao conjunto N segundo ela o zero pertence ao conjunto Z e não pertence ao conjunto N. Será que ela sabe o que está dizendo? É preocupante. Será que Maria é professora de Matemática e desconhece o assunto? Se for realmente sem chance nem para ela nem ninguém.
quero parabenizar a voces pelo site e gostaria de receber exercicios resolvidos de conjuntos numericos.desde ja obrigado.
gostei muito do site é informativo, para pesquisas e etc
Achei o site legal, mas poderia ter exercícios resolvidos para exemplificar os tipos de conjuntos numéricos.
é claro que o N tem 0, assim como Z
gostei do site também e gostaria de receber as definições dos 5 conjuntos, mais detalhadamente:
achei super legal o site, e gostaria que se possível me fosse enviado tudo sobre o conjunto dos numeros inteiros operações e propriedades
obrigado,
josé
ola gostaria q vcs mandase por mail 5 exemplosde cada tipo de numeros racionais inteiro,decimalexato e dizima periódica. e fazer o mesmo p o numero irracional obrigado estor precisando com um certa urgencia boa noite.
gostaria de saber noticia que tenha numeros negativos por favor mande para mim
Eu simplesmente não gostei, mas não vi nenhum erro nele, não gostei foi da simplisidade do blog, valeu, poderia melhorar as cores por mais alguns exmplos, o restante esá ok, um abraço Professor Jozivaldo de Física, Matemática e Informática…
Recife – PE
oi!!gostaria de saber os numeros naturais interios:operaçoes,relaçoes de ordem,divisibilidade….agradeço pela atençao,pois os trabalhos de vcs sao maravilhosos.
gostaria de saber os conjuntos de q
12. JOILSON T. DOS SANTOS | Abril 6th, 2007 at 20:27:52
EU GOSTARIA DE SABER EM QUE É APRICADO
CONJUNTO DOS NUMEROS INRRACIONAIS
INRRACIONAL ?! Onde é aplicado ? … Apricra isso na sua burrice !
Nossa ..
achei mt leve o blog! diferente das teorias matemáticas, por vezes pesadas para os leigos… ou iniciantes!
preciso fazer um trabalho de matemática sobre a origem dos conjuntos numéricos. se alguem quiser me ajudar mandando alguns sites contendo o assunto fico grata!
msn:
pri_cila15@hotmail.com
Obrigada.
quem quizerr entrar em contado meu e-mail é;
ti_a_silva@hotmail.com
sou estudante de matemática e estou no meu primeiro a no de faculdade.Gostaria de conhecer pessoas que se interessem pela materia para podermos trocar conhecimentos.
Se alguém puder , por favor entre em contato atraves de meu e-mail!
muito obrigado!
antes de fazer um comentário em um site de matemática, vcs – bruna rodrigues, ronqui e joilson – deviam ir a um site de português. tudo bem. eu não sou nenhum expert em Português, mas pra escrever como vcs escrevem tem q ser um artista…….
no mais, mto bom esse site….gostei !!!!!
EU GOSTARIA DE SABER EM QUE É APRICADO
CONJUNTO DOS NUMEROS INRRACIONAIS
Olá, gostaria de parabenizar e agradecer o site pelas publicações. Também notei que para o conjunto dos irracionais não foi atribuído nenhum símbolo q o representa-se, pesquisei em outros sites e encontrei o “I” como símbolo dos irracionais, esta simbologia está correta? Grato.
OSITE É BEM EXPLICATIVO,MAS CADÊ O SIMBOLO DOS IRRACIONAIS?
EX:N de naturais
é prescisei desse intério para meu trabalho e gostei ,não sei se era tudo que prescissava mas só digo que gostei
grata
bruna rodrigues!
obrigado pela atenção de todos que leram este comentário.
hi esse site não té com nada
gostei muito da expressao de explicar o conteudo esta muito bem explicado ok continue assim.
Se o conjunto dos naturais não contem o zero, qual a definição do IN*?
estou com dúvidas em relação aos intervalos entre os números reais. Seria possível me enviarem exercicios resolvidos , não consigo entender o que intervalo aberto ou fechado. Me ajudem!
eu gostei deste site, mas gostaria de receber via e-mail, o mais rápido possível cinco exemplos dos conjuntos numéricos ( cinco de cada ) espero ser socorrido.
obrigado e fui!!!
Eu particularmente gostei deste site.
Mas,olhando os comentários,percebi q realmente existem erros quanto ao ensino dos conjuntos dos números naturais.
E sendo assim,serei mais uma pessoa pedindo para que consertem o erro!Ok?
Beijos =*
Fernanda,15 anos
Quero que me envie por est e-mail, execícios de exemplo, resolvidos sobre Conjuntos Numéricos, Cálculo I, II,III, ficarei muito feliz por t me ajudado…
Até mais… E um abraço…
Eu pessoalmente gostei muito do site, mas, vocês deram um erro pois o conjuno dos números naturais não tem zero!! o conjunto dos números inteiros é que tem!!! recomendo que corrijam este erro pois se alguém precisar de fazer algum trabalho, ele vai ficar errado!!
Maria, 13 anos, 12-02-07